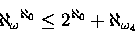 kifejezés áll.
kifejezés áll. Igen, ez a tétel a könyvem utolsó fejezetében szerepel.
Saharon Shelah 2000 novemberében azért látogatott Magyarországra, hogy átvegye az első megújított Bolyai János Nemzetközi Matematikai Díjat. A Bolyai-díjat a Magyar Tudományos Akadémia 1902-ben alapította. Az első díjazottak Henri Poincaré és David Hilbert, a korszak legnagyobb matematikusai voltak. A Magyar Tudományos Akadémia most megújította a díjat, és ötévente kívánja jutalmazni vele a "megelőző tíz évben megjelent legkiválóbb, áttörő jelentőségű, saját új eredményeket, módszereket bemutató matematikai monográfia" szerzőjét.
Kezdjük az elején. Hogyan találkozott a matematikával?
Anyám szerint megszámoltam a mintákat a padlón, bár én ezt kétlem. Általános
iskolás koromban nem érdekelt különösebben a matematika. Ötödikes voltam,
amikor elkezdtem érdeklődni a természettudományok: a fizika, a csillagászat és
a biológia iránt, nyolcadikban pedig fizikai kísérleteket végeztem.
Középiskolás koromban jártam egy évig kémiai és egy évig biológiai
laboratóriumba.
Tagozatos osztályba járt?
Nem, Izraelben akkoriban még nem létezett ilyesmi. Szóval, amikor a
laboratóriumba kerültem, rájöttem, hogy ez nem nekem való. Közben viszont
megszerettem az euklideszi geometriát. Nagyon tetszett az axiómarendszer
gondolata, mert korábban a matematika számomra csak a számolást jelentette.
Esetleg már az euklideszi geometriában is a párhuzamossági axióma
függetlensége érdekelte?
Nem, odáig nem jutottam el. Hallottam róla, de nem találtam olyan könyvet, ahol
utána tudtam volna nézni. Az nyűgözött le az euklideszi geometriával
kapcsolatban, hogy egy kis axiómarendszerből kiindulva mindent be lehet
bizonyítani. És maga a bizonyítás gondolata is megfogott, ugyanis a
számolásokat az ember vagy elrontja vagy nem, de egy bizonyítás tiszta ügy.
Honnan tanult?
A középiskolás tanárom ajánlott egy nagyon jó könyvet. Aztán volt egy
középiskolásoknak szóló matematikai folyóirat is, ami évente négyszer jelent
meg, és cikkeket, feladatokat tartalmazott. Ezt a végén én osztogattam az
iskolában.
A természettudományos érdeklődés családi vonás?
Egyáltalán nem. Értelmiségi volt a családom, de tisztán humán beállítottságú.
Igaz, apámnak középiskolás korában jól ment a matematika, ezenkívül a
nyelvészet is érdekelte, ami bizonyos értelemben közel áll a
természettudományokhoz.
Az egyetemen alkalmazott matematikát kezdett tanulni.
Már középiskolás koromban tudtam, hogy az elméleti matematika érdekel, de Tel
Avivban - ahol laktam - csak alkalmazott matematika szak volt. Akkoriban a Tel
Avivi Egyetem még csak félig létezett, abban sem voltunk biztosak, hogy a végén
megkapjuk a BSci fokozatot. Mindenesetre már Tel Avivban is az absztrakt
matematika érdekelt, és úgy tudtam, hogy a logika a matematika legabsztraktabb
ága. Ezért döntöttem a logika mellett. Az MSci fokozatot már Jeruzsálemben
szereztem meg elméleti matematikából. Ez elég komplikált volt a katonaság
miatt. Ugyanis egy évig voltam katona érettségi után, de a maradék két évet az
egyetemi évek alatt töltöttem le. Katona Tel Avivban voltam, miközben
Jeruzsálembe jártam egyetemre. A BSci fokozatomra való tekintettel minden
csütörtököm szabad volt, tehát az egyetemen azokat az órákat választottam, amik
csütörtökön voltak.
A doktori disszertációját is Jeruzsálemben írta.
Igen, modellelméletből, ami a logika egy ága. Aztán külföldre kellett mennem,
mert Izraelben az a szabály, hogy a kutatóknak a doktori iskola után néhány
évet külföldön kell tölteniük. Én Princetonba mentem. Ez nagyon jól mutat az
önéletrajzomban, de más hasznot nem igazán hozott, mert az ottani
logikaprofesszor épp kutatói szabadságon volt. Ezután a kaliforniai UCLA
egyetemen dolgoztam, ahol nagyon jó társaságom volt matematikai szempontból.
Ott találkoztam például Fred Galvinnal, aki bizonyos értelemben Erdős
tanítványa volt. Tőle partíciókalkulust tanultam, ami a halmazelmélet egy ága.
És azután?
Visszamentem a jeruzsálemi Héber Egyetemre, és azóta is ott dolgozom.
Úgy tudom, hogy a Rutgers egyetemmel is van kapcsolata.
Igen. Szeptemberben és októberben nyári szünet van Izraelben, és ilyenkor a
Rutgersen tartok egy kutatószemináriumot. Ezenkívül a cikkeimet mindig a
Rutgersre küldöm gépelni.
A Rutgersen jobban gépelnek a titkárnők?
A Héber Egyetemen okosabbak a titkárnők, és nem hajlandók begépelni a cikkeimet.
Olyan csúnyán ír?
Nem, hanem rengeteget javítgatok, ezért nehéz kiigazodni a kézirataimon.
Egyébként Jeruzsálemben időnként megbízok külsős gépírónőket.
Ha a nyári szünetben a Rutgersen dolgozik, akkor mikor pihen?
A Rutgersen csak felsőbbéveseket tanítok, ezenkívül látogatóim vannak, akikkel
együtt dolgozunk. Örülök, hogy több időm van kutatni, mint máskor.
Mennyi időt tölt kutatással?
Erre nagyon egyszerű válaszolni. Hat napot dolgozom egy héten. Reggel 9-re
megyek be az egyetemre, és este 7-ig vagyok ott. Aztán hazamegyek, ahol a
feleségemmel beszélgetek és olvasok.
Jól tudom, hogy a felesége magyar?
Igen, nyolcéves koráig Magyarországon élt. Nem tudom megítélni, de szerintem
jól beszél, ír és olvas magyarul.
A gyerekei mivel foglalkoznak?
A nagyobbik fiam zeneelméletet tanul, a lányom történelmet, a kisebbik fiam
pedig biológiát. Nagyon szeretem őket, és nagyon szeretek velük lenni. Viszont
egyikük sem szeretett bele a matematikába.
Szoktak Magyarországra látogatni?
Igen, többször is voltunk itt a feleségemmel. Meglátogattuk a rokonait,
elmentünk azokra helyekre, amelyek gyerekkorából fontosak voltak neki.
Megnéztünk néhány nevezetességet is, például a gyönyörű Mátyás templomot.
Legtöbbször viszont egyedül jövök Magyarországra. Sok magyar matematikussal
dolgoztam együtt, először Erdőssel. Őt rengeteg minden érdekelte, és ezek közé
tartozott a halmazelmélet is, elsősorban a partíciókalkulus. Aztán Fred
Galvinnal is együttműködtem, aki bár amerikai, sok köze van Magyarországhoz.
Rajtuk kívül sokat dolgoztam és dolgozom Bíró Balázzsal, Hajnal Andrással,
Juhász Istvánnal, Komjáth Péterrel és Sokoup Lajossal.
A Rutgersen is sok magyar matematikus van. Közülük foglalkozik valaki az ön
témájával?
Hajnal. A többiek véges kombinatorikával foglalkoznak. Bár Erdőssel dolgoztam
valamennyit véges kombinatorikán, ez nem az én szakterületem.
Izraelben Erdős-díjat kapott.
Ez a díj valójában Erdős szüleinek a nevét viseli. Ő alapította, de nem akarta
saját magáról elnevezni. Olyan fiatal matematikusok kapják, akiknek közük van
az elméleti számítástudományhoz. Azt hiszem, én kaptam az elsőt.
Mint ahogy ön kapta az első megújított Bolyai-díjat is. Az első világháború
előtt ezt a díjat Poincaré és Hilbert kapták meg.
Ez hatalmas megtiszteltetés számomra.
Tudta, hogy a következő díjazott Einstein lett volna?
Valóban? Ezt nem tudtam. Remélem, nem rontom majd el a díj jó hírét. Időbe
kerül, amíg egy ilyen díj hírneve újraéled, de az első két díjazott
felülmúlhatatlan. Hilbert és Poincaré nagyon nagy emberek voltak, de csak a
matematikusok tudnak róluk. Érdekes, hogy miért van az, hogy ha valaki nem
tudja, ki volt Beethoven vagy Bach, akkor műveletlennek tartják, míg a
matematikusokkal kapcsolatban ez nem így van.
Most olvastam egy cikket, ami a zenét és a matematikát párhuzamba állítva
ugyanezt a kérdést tette fel.
Ez nagyon érdekes. És milyen következtetésre jutottak?
Hogy a matematikaoktatásban van a hiba, mert érdekes dolgok helyett csak
számolni tanulnak a gyerekek.
Ez igaz, de a zenetanulás során is rengeteg unalmas ujjgyakorlatot kell
végezni. Szerintem az a fő különbség, hogy a matematikát csak olyan ember tudja
értékelni, aki ért is hozzá. Ha az ember nem élvezhetné a zenét anélkül, hogy ő
maga is jól zenélne, a zeneszeretők száma drasztikusan csökkenne.
Egyébként azért is örültem ennek a díjnak, mert amikor az ember elmúlt 50 éves,
akkor általában az életművéért kap díjat. Ezt a díjat viszont egy tíz évvel
ezelőtti eredményemért kaptam, nem pedig huszonévesen kitalált dolgokért.
A díjat Számosság-aritmetika című könyvéért kapta. Mi ennek a témája?
Száz éve Cantor felfedezte, hogy többféle végtelen van, és hogy ezekkel
számolni is lehet. Először felállította az összeadás és a szorzás szabályait.
Ezekkel egyébként az iskolás gyerekek nagyon elégedettek lennének, ugyanis két
végtelen szám összege is és szorzata is megegyezik a nagyobbik számmal. A
hatványozás kérdése azonban megoldatlan maradt. Cantor kimondott egy sejtést,
amely szerint a hatványozás is nagyon egyszerűen működik, ez a kontinuum
hipotézis, illetve az ennél általánosabb általánosított kontinuum hipotézis. Ez
a sejtés nagyon természetes volt, és Hilbertnek ez volt az első kérdése azon a
listán, amely a matematikusok huszadik századi házi feladatát tartalmazta.
Később Gödel bebizonyította: nem lehet bebizonyítani, hogy ez a sejtés hamis.
Aztán a hatvanas évek elején Paul Cohen bebizonyította, hogy bebizonyítani sem
lehet ezt a sejtést.
Tehát a matematika úgy is működik, hogy feltesszük, ez a sejtés igaz, és úgy
is, ha feltesszük, hogy nem igaz. Erre mondjuk azt, hogy az állítás független a
matematika többi szabályától.
Vagyis a dolgok kaotikusak. Sok ehhez hasonló eredmény született. Ugyanakkor
felfedezték, hogy vannak bizonyos megkötések. A hetvenes évek közepén sokan
foglalkoztak ezzel a témával, például Silver, Galvin és Hajnal. Nekem is nagyon
érdekesnek tűnt, sajnáltam, hogy túl későn kapcsolódtam be ebbe a kutatásba.
Pár évvel később az lett az általános vélemény, hogy a kontinuum hipotézis
függetlensége nagyon fontos eredmény, de ez a témakör lényegében már ki van
végezve, már csak be kell látni mindenről, hogy független. Így néhány évvel
később már úgy éreztem, hogy egyedül engem érdekel ez a dolog.
1980 és 1982 között lényegesen megváltozott a képem a témakörről. Amire akkor
jöttem rá, arról írtam később a könyvet. A lényeg az, hogy külön kell
választani két dolgot. Az egyik a hatványozás, ahol az úgynevezett reguláris
számosságok esetében van néhány egyszerű szabály, és tudjuk, hogy több
szabályosság nincs. Másrészt viszont ha nem a hatványozást vizsgáljuk, hanem
végtelen sok szám szorzatát, akkor vannak szabályok. Az eredmény ugyan most sem
egyértelmű, de meg tudjuk adni a lehetséges eredmények egy halmazát. Mint
amikor a diofantoszi egyenletek megoldása nem egy szám, hanem több lehetséges
érték, de ezeket ismerjük. Tehát ezen a módon egy olyan számosság-aritmetikához
jutunk, ahol ugyan nem lehet mindent eldönteni, de a válaszok mégis inkább
"igen-nem", mint "nem tudni" természetűek. Ez a PCF elmélet (potential
cofinality - lehetséges kofinalitás), amiről a könyvet írtam.
A honlapja tetején az 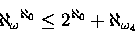 kifejezés áll.
kifejezés áll.
Igen, ez a tétel a könyvem utolsó fejezetében szerepel.
Ez a legfontosabb eredmény?
Nem mondanám, hogy a legfontosabb, de talán a leglátványosabb, ez ragadja meg
legjobban az elmélet lényegét.
A PCF-elmélet előtt ön fejlesztette ki a proper-forszolás elméletét. Ez a
PCF-elmélettel ellentétben függetlenség megmutatására szolgál.
A proper-forszolás egy általános módszer függetlenség megmutatására. Persze
minden egyes kérdést egyedien kell bizonyítani, de vannak olyan általános
eszközök, amelyek a munka egy részét elvégzik helyettünk.
Egyébként ellentmondásosnak tűnik, hogy miért akarja valaki belátni, hogy egy
kérdés eldönthetetlen. A feleségem néha viccelődik azon, hogy olyan ez, mintha
két hadsereg állna egymással szemben: az egyik a függetlenségért, a másik a
válaszokért harcol. Szerintem sokkal jobb megoldani egy kérdést, mint azt
mondani, hogy nincs válasz, de ha már az utóbbi az igazság, mégiscsak jobb
tudni. Hasonlóan, mint amikor Erdős egyszer 100 dollárt ajánlott egy állítás
bizonyításáért, és 25-öt egy ellenpéldáért. Annak örült volna igazán, ha valaki
bebizonyítja az állítást, de azt is tudni szerette volna, ha az állítás hamis.
Képzeljük el például, hogy van egy listánk száz kérdéssel, amelyek közül a
legtöbb eldönthetetlen, de van köztük öt gyönyörű eldönthető állítás. Ha valaki
nem tudja, hogy a maradék kilencvenöt kérdésre nincs válasz, akkor elpocsékolja
rájuk az erejét, és esetleg nem jut el az öt szép állításhoz. Tehát a
függetlenségi bizonyítások segítségével meg lehet tisztítani egy területet az
eldönthetetlen kérdésektől. Ha utólagos bölcsességgel nézem - és utólag mindig
nagyon bölcs az ember - akkor azt mondhatom, hogy így volt ez a
számosság-aritmetika esetében is.
Ismerte Paul Cohent, a forszolás atyját?
Hát találkoztam vele tíz évvel ezelőtt egy egyetem folyosóján, és egy-két
hónapja is összefutottunk Svédországban.
Annak ellenére, hogy az ő munkáját folytatta, nem volt vele
kapcsolata?
Cohen rengeteg témán dolgozott. Miután kitalálta a forszolást és ezzel belátta
a kontinuum hipotézis függetlenségét, mással kezdett foglalkozni: egy
Lebesgue-mérhetőséggel kapcsolatos kérdéssel.
Cohen egy interjúban ezzel a kérdéssel kapcsolatban az ön nevét is
említi...
A kérdést Solovay oldotta meg, de felhasznált hozzá egy külön feltételt. Az
volt a kérdés, hogy erre a feltételre szükség van-e. Erre válaszoltam én.
Szemmel láthatóan sok témával foglalkozott. Összefoglalná, hogy mik voltak
ezek a területek?
A szakdolgozatomat modellelméletből írtam, ezenkívül a végtelen kombinatorika
is érdekelt. A doktori iskolában szintén a modellelmélettel, illetve elsőrendű
logikával foglalkoztam. Az volt a célom, hogy a különböző elméleteket úgy
rendszerezzem, ahogyan a rendszertan az állatokat például az emlősök vagy a
rovarok osztályába sorolja. Később - ezen sokan megütköztek - a
partíció-kalkulus is érdekelt. Azután foglalkoztam általános végtelen
kombinatorikával, forszolással és a számosság-aritmetikával, ami valójában a
kombinatorika egyik ága. Egy keveset véges kombinatorikán, illetve a matematika
néhány más területén is dolgoztam.
Melyik eredményére a legbüszkébb?
Erre nehéz válaszolni. Olyan, mint ha azt kéne megmondanom, hogy melyik
gyerekemet szeretem a legjobban. Talán a PCF-elmélet, de hát ebben a témában
éppen most vagyok a kutatásaim tetőfokán. Ezenkívül van egy modellelméleti
tételem is, amire büszke vagyok.
Matematikusokkal kapcsolatban használják a problémamegoldó és az
elméletépítő megkülönböztetést. Önt mind a kettőnek tartják.
Remélem. Számomra egyébként ez a két dolog nem válik teljesen külön. Az
elméletek ugyanis gyakran egy konkrét kérdés megoldásából születnek. Amikor azt
a módszert, amit a kérdés megoldásához használtunk, más kérdésekre is
alkalmazzuk, akkor elméletté válik. Például azt hiszem, hogy a PCF-elmélet
segítségével lehet a kombinatorikus halmazelméletben is általános módszereket
keresni. Persze vannak olyan területek, mint például a kombinatorika, ahol az
ember jellemzően nem magas tornyokat épít, hanem inkább különálló kérdéseket
old meg. De ez sem fekete-fehér igazság, hiszen ott is vannak általános
módszerek.
Szerintem azok a jó sejtések és a jó kérdések, amelyek megoldása elméletek
építésére kényszeríti az embert. Vegyük például Hilbert listáját a
matematikusok huszadik századi házi feladatával. Ennek a listának szerintem
nemcsak azért lett olyan nagy jelentősége, mert majdnem mindegyik probléma
nagyon nehéz volt, hanem azért is - legalábbis azokban a témákban, amikhez
értek - mert a megoldásukhoz új elméleteket kellett kiépíteni. Például Cohen
nem csupán megoldotta Hilbert első kérdését, de a megoldásából nőtt ki az az
egész elmélet, amiről a könyvemet írtam. Ha a lista túl nehéz feladatokat
tartalmazott volna, akkor lehet, hogy csak tízezer év múlva oldották volna meg
őket, és semmi hasznunk nem lenne belőle. Egy kevésbé nyilvánvaló hiba az
lehetett volna, hogy sokat kellett volna dolgozni a megoldásokon, de közben a
válaszokon kívül semmit sem tudtunk volna meg.
Egyébként én a magam részéről nagyon szeretek problémákon gondolkozni, különben
miért is lennék matematikus? Aztán így lehet igazán megérteni, hogy mások
mivel foglalkoznak. Még ha nem is sikerül megoldanom a kérdést, akkor is jobban
megértem a téma természetét. Ugyanakkor szeretek általános módszereket is
kifejleszteni. Ez gyakran úgy történik, hogy egy konkrét kérdésen gondolkozom,
és eljutok valameddig, de a megoldásom nem teljes. Ilyenkor el kell mélyítenem,
tovább kell fejlesztenem azt a módszert, amit használok. Így alakult ki a
forszolásból a proper-forszolás. Vagy például egyszer valaki feltett nekem
néhány Boole-algebrákkal kapcsolatos elég speciális kérdést. Az egyik kérdés
megoldásánál felhasználtam egy állítást, amit korábban a
számosság-aritmetikával kapcsolatban bizonyítottam be. Annak idején ez csupán
egy segédállítás volt, egy bizonyítás építőeleme, de ekkor kiderült, hogy
sokkal általánosabban felhasználható.
Mit csinál, amikor matematikán gondolkozik?
Általában járkálok, vagy babrálok valamivel, ahogyan most is. Nem dohányzom, a
babrálás viszont ártalmatlan. Amikor valami eszembe jut, rögtön leírom. Azt
hiszem a legtöbb matematikus nem így csinálja, hanem csak akkor ír le valamit,
ha már kész van a bizonyítás. Úgyhogy rengetegszer megtörténik, hogy írok
valamit, aztán kidobom a kukába. Máskor nem jön ki valami, de úgy gondolom,
hogy az ötlet alapjában véve jó. Ilyenkor visszamegyek, megváltoztatom a
bizonyítást, megváltoztatom a definíciókat, és a cikk egyre bonyolultabb, tele
van átfirkálásokkal és kiegészítésekkel, és amikor úgy gondolom, hogy már jó,
akkor elküldöm a titkárnőnek. Ez talán megmagyarázza, hogy miért nem vagyok
népszerű a titkárnők körében.
Azt mondják, hogy a ma élő matematikusok közül önnek van a legtöbb
cikke.
Hallottam, hogy egy budapesti honlapon van egy lista erről, és hogy Erdős
magasan vezet. Egyébként neki még mindig jelennek meg cikkei, pontosabban
olyanok, amiket a társszerzői írnak le. Azt is hallottam, hogy a listán én is
elég előkelő helyen állok. Persze nem attól lesz valaki jó matematikus, hogy
sok cikke van. Viszont azokat sem értem, akik szerint baj, ha valaki túl sok
cikket ír. Mi abban a rossz, ha az ember leír érdekes, de nem fontos
eredményeket is?
Az egyetemen nem szokták megzavarni, miközben dolgozik?
Nem. Legfeljebb az szokott előfordulni, hogy gondolkodom valamin, közben valaki
bejön, és feltesz egy érdekes kérdést, amit aztán együtt próbálunk megoldani.
Meg aztán nem vagyok valami rendes, és ezért nem vagyok tagja túl sok
bizottságnak.
Sokat dolgozik együtt másokkal?
Ha Erdőshöz hasonlítjuk, valószínűleg kevésnek tűnik, de egyébként azt hiszem,
igen. Amikor egyedül dolgozom, nagy csatákat vívok a leírással, bizonyítással.
Ha másokkal dolgozom, az azért is jó, mert akkor csak a fejemet kell törnöm, és
a munka kellemetlen része, például a cikkírás nem az én dolgom.
A fő témáján inkább egyedül gondolkodik?
Nem is tudom. Talán a cikkeim felét írtam másokkal, a hosszabb dolgokat viszont
egyedül. Vannak olyan témák, amelyek nagyon érdekelnek, és még akkor is
hajlandó vagyok rajtuk egyedül gondolkodni, ha egyébként nem túl népszerűek.
Ilyenek a könyveim is. Egy kérdést megoldok azért, mert valaki megkért rá, de
egy könyvet nem fogok csak ezért megírni.
Tehát amikor másokkal dolgozik akkor általában az történik, hogy ők
kérdeznek és ön válaszol?
Igen. Azt szoktam mondani, hogy jobb vevő vagyok, mint eladó. Ez nem azt
jelenti, hogy jobb vagyok problémamegoldásban, mint kérdésfeltevésben.
Szerintem csodálatos kérdéseim vannak, csak erről nem tudok másokat meggyőzni.
Ez persze nem mindig van így, főleg a diákok esetében nem. Lehet, hogy a
kérdéseim nem elég meggyőzőek, vagy túl nehezek, de az biztos, hogy nem vagyok
sikeres ezen a téren. Így hát igaz, hogy sok emberrel dolgozom együtt, de
legtöbbször azon gondolkodunk, ami a többieket érdekli.
Én ezt nem nevezném kudarcnak. Inkább úgy látom, hogy mások használják ki
önt, és nem fordítva.
Nekem is hasznos, ha kérdeznek tőlem. Egyrészt a matematikának sok nagyon szép
ága van, és azáltal, ha feltesznek nekem egy kérdést, megismerhetek egy új
területet. Így hát még akkor sem vagyok csalódott, ha nem sikerül válaszolnom.
Másrészt egy módszeremről akkor derül ki igazán, hogy hatékony, ha valaki
másnak a kérdését oldom meg a segítségével. Ráadásul így talán sikerül valakit
meggyőznöm, hogy olvassa el egy könyvemet. Ez ugyanis gyakran nehezebb, mint
elnyerni egy díjat. Ha viszont nem sikerül válaszolnom egy kérdésre, akkor
sokszor az derül ki valamelyik módszeremről, hogy jó, de még élesítenem kell,
tovább kell fejlesztenem.
Szeret tanítani?
Nem szeretek olyan diákokat tanítani, akik jegyet akarnak. Mármint akik csak
jegyet akarnak. Az még önmagában nem baj, ha valaki jegyet is akar, én is
elvárom, hogy megkapjam a fizetésem azért, hogy matematikán gondolkodom. Az
elsőévesek többsége viszont csak jegyet akar. A Logika 2 előadás, ahol például
Gödel nemteljességi tételét tanítom, már jobb. Nem mondom, hogy ennek a
tárgynak a hallgatói különlegesen érdeklődnek, de azért akarnak tanulni. Igaz,
hogy ezt az előadást sem vállalnám el önként.
Tehát alsóbbéveseket is kell tanítania?
Attól függ, mire van szükség az egyetemen.
Vannak olyan diákjai is, akiket mélyebben érdekel a témája?
Az évek során több diákot érdekelt annyira a témám, hogy nálam írták a doktori
disszertációjukat. Ennek örülök.
Mit gondol Erdősről?
Erdős nagyszerű volt. Vicces ember volt, például harmincéves korától fogva öreg
embernek hívta magát - ettől mondjuk nem voltam elragadtatva. Rendkívül jószívű
volt. Az is nagyon tetszett benne, hogy mennyire szerette a matematikát, szinte
már szélsőségesen. Én azért meg akartam nősülni, és gyerekeket akartam. Erdős
ezenkívül nagyon fontos új területeket és módszereket talált ki. Ezek között
persze sok olyan van, amihez nem értek. Például a számelméleti eredményeit csak
hírből ismerem. Két olyan területhez értek, ahol Erdős nagy dolgokat hozott
létre. Az egyik a valószínűségi módszer, amit csodálatosnak tartok, és én is
használtam. A másik a partíció-kalkulus a halmazelméletben, ami nemcsak a
módszereit, de bizonyos értelemben a létét is neki köszönheti. Én a
halmazelmélettel akkor kerültem kapcsolatba, amikor észrevettem, hogy a
modellelméletben szükség van a partíciókalkulusra.
Erdősnek az is érdeme, hogy a matematikát társaságibbá tette. Ugyanis a közös
cikkek hátterében gyakran nem igazi közös munka áll. Időnként két egymástól
teljesen függetlenül dolgozó ember észreveszi, hogy hasonló eredményeik vannak,
úgyhogy közösen leírják. Vagy egy diák és a témavezetője írnak közös cikket.
Ezek is jó dolgok, de más, mint az Erdős-féle közös munka, amikor az emberek
tényleg együtt ülnek és gondolkodnak. Az egyik barátom egyszer kérdezett
valamit egy matematikustól, aki azzal a feltétellel válaszolt, hogy másoknak
nem mondja el. Ez a hozzáállás a matematikának mindenképpen rossz, de szerintem
magának a matematikusnak sem jó, mert ha valamit mással is megbeszél, akkor ő
maga is jobban megérti.
Erdős érdemei közé tartoznak a feladatsorai is. Ezeket diákok számára írta
azzal a céllal, hogy feladatokon keresztül sajátítsanak el egy bizonyos
témakört.
Mit csinál, amikor nem matematikával foglalkozik?
Szeretek regényeket vagy történelmet olvasni, beszélgetni a feleségemmel és a
barátaimmal. Viszont nem igazán szeretek várost nézni és kirándulni. Ha
külföldön vagyok, akkor szívesebben beszélgetek az országról az ott élő
emberekkel.