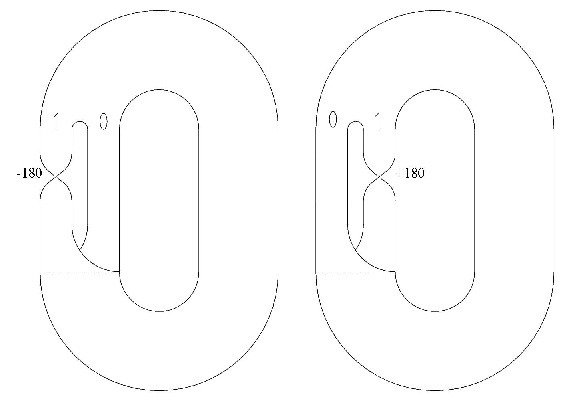
1. ábra. A Rössler-rendszer (bal oldal) és a W Virginis-modell (jobb oldal) attraktora. A templét a szaggatott vonal mentén összeillesztett két szalagból áll
Kepler bolygómozgási törvényeiben az égitestek mozgásában uralkodó rend mutatkozik meg. A tökéletes rendet keresve jutott el Kepler a szférák zenéjének ideájáig is. Ma már tudjuk, hogy az égi mechanika nem csak reguláris pályák létét teszi lehetővé, hanem gyakrabban találhatunk kaotikus mozgásokat. Ha a szférák zenéjéhez keresünk megfelelő hangszereket, nem is kell elhagynunk a csillagászat területét. Kepler még nem tudhatta, de ma már nyilvánvaló tény, hogy egyes változócsillagok fényváltozását a csillagok akusztikus oszcillációi okozzák. A hullámmozgások hasonlósága révén tervezhetünk olyan trombitát, amelynek lehetséges hangmagasságarányai nagyon jó közelítéssel egyeznek egy csillag sajátrezgéseinek frekvenciaarányaival. Természetesen a frekvenciák értékében több nagyságrendnyi eltérés van, de megfelelő skálázással hallhatóvá tehetők akár a csillagok rezgései is. A csillagászokat sokáig elsősorban a szabályosan lüktető változócsillagok érdekelték, hiszen egyszerűbb volt értelmezni őket, így használhatóvá váltak egyebek között a csillagászati távolságskála felépítésében. A szférák zenéjének kaotikus dallamaihoz viszont mind elméletileg, mind a megfigyelésekben megtaláltuk a megfelelő hangszereket, azaz a kaotikusan pulzáló csillagokat. A Magyar Tudomány káosszal foglalkozó korábbi számában az első eredményeket ismertettem (Kolláth, 1993). Az elmúlt évtizedben újabb darabkák illeszkedtek a csillagászati események kaotikus kirakójátékába.
A csillagászati adatok feldolgozása különleges kihívást jelent még a nem kaotikus jelenségek elemzésekor is, hiszen sok esetben csak korlátozott időtartamú, erősen zajos idősoraink vannak. Gondoljuk csak el, hogy a kaotikus folyamatok szempontjából érdekes sok változócsillag periódusa éves nagyságrendű, ezért több évtized hosszúságú folytonos megfigyelési sorozatokra van szükségünk. Egy ilyen beláthatatlan végű megfigyelési program megkezdése - különösen a mai tudományfinanszírozási körülmények között - reménytelennek tűnik. Műkedvelő és amatőr csillagászok viszont kedvtelésből elvégezték, és napjainkban is folytatják csillagok százainak fénybecslését. Az így megkapható adatsorok hossza és mintavételezése sok esetben megfelel a kívánalmaknak, a jel/zaj viszony azonban már korántsem tekinthető biztatónak. Egy másik érdekes jelenség a naptevékenység változása, amelynek domináns periodicitása 11 év. Emberöltők szükségesek ahhoz, hogy értelmezhető hosszúságú nyersanyaghoz juthassunk. További nehezítő körülmény, hogy a megfigyelhető jelenségekből kapott számszerűsíthető mennyiségek, például a napfoltszám és a folyamatok hátterében álló fizikai folyamatok között meglehetősen kusza a kapcsolat. A megfigyelési zajhoz ráadásul belső, a Nap működéséhez kapcsolódó zajok is társulnak, pl. a konvekció által.
Az égi mechanikához kapcsolódó kaotikus jelenségek majdhogynem a napi sajtó hírei közé is bekerültek a földközeli kisbolygókkal kapcsolatban. Amikor azzal riogatják az olvasókat, hogy az adott kisbolygó pár száz év elteltével összeütközhet a Földdel, a pontos előrejelzés bizonytalansága a pálya összetettségéből és a jelenlegi pályaelemek pontatlanságából tevődik össze. A nagyközönséget is érdeklő másik terület a más csillagok körül keringő bolygórendszerek, amelyekből az utóbbi években többet is találtak. A jelenlegi megfigyelési technikával csak a nagyobb, Jupiterhez hasonló tömegű bolygók mutathatók ki. Ha ismerjük az ilyen nagyobb bolygók pályáját, akkor viszont ellenőrizhető, hogy a lakható tartományban (ez persze antropocentrikusan definiált) stabilak-e a lehetséges bolygópályák. Ezen a területen hazai kutatások is folynak (l. Sándor Zsolt és munkatársai 2000). A vizsgált bolygórendszerek között vegyesen vannak olyanok, amelyekben stabilak és amelyekben instabilak a Föld típusú planéták pályái.
Az előző cikkemben (Kolláth 1993) több egyszerű kaotikus folyamatot ismertettem a csillagok világából, ezek többsége segítséget nyújthat a kaotikus rendszerek folyamatainak megértéséhez. E cikkben az adatfeldolgozásra helyezem a hangsúlyt, talán a csillagászatban elterjedőben lévő módszerek így más területeken is használhatóvá válhatnak. Saját kutatásainkban két módszert alkalmazunk rendszeresen, a globális fázistér-rekonstrukciót és az idő-frekvencia-eloszlásokat. Mindkettő hatásosnak bizonyult csillagászati adatsorok esetére is.
Globális fázistér-rekonstrukció
Amennyiben egy idősor determinisztikus, kevés szabadsági fokú folyamat eredménye, akkor az adatsort létrehozó dinamikai rendszer legtöbb tulajdonsága rekonstruálható. Elegendő egydimenziós adatsorból kiindulnunk, hiszen a Takens-tétel, illetve annak kiterjesztései alapján egy d-dimenziós áramlás definiálható az s(t) idősorból, ahol d a beágyazási dimenzió.
A megfigyelésekből előálló fázistérbeli áramlás az x(t) vektorral reprezentálható, ami diszkrét mintavételezés (ti=t0 + i Delta t) esetén az x(i)= x(ti) mennyiségekkel adott. A vektor komponensei az általánosan használt időeltolás módszerével adottak: x(i)={s(ti), s(ti+tau),..., s(ti+(d-1))}. Amennyiben az adatsorból rekonstruált fázistér dimenziója elegendően nagy ahhoz, hogy a rekonstrukció egyértelmű legyen, akkor a rendszer determinisztikus volta miatt léteznie kell az áramlást definiáló differenciálegyenlet-rendszernek:
dx(t) / dt = f(x(t))
ami ekvivalens egy leképezéssel:
x(i+1) = F(x(i) )
Feltételeztük, hogy az f és F függvények explicit módon nem tartalmazzák az időt, ami egy pulzáló csillag esetén azt jelenti, hogy a megfigyelések időintervallumán a csillag fizikai paraméterei állandóak, azaz a fejlődési effektusok elhanyagolhatók. Valamilyen funkcionális formát feltételezve a leképezés illeszthető legkisebb négyzetes illesztéssel. Az általunk vizsgált esetekben a leképezés Fj komponenseit (F ={F1, F2 ,..., Fd }) polinomiális alakban keresve megfelelő eredményeket kaptunk.
A leképezés önmagában még nem jelent használható információt. Az illesztett leképezés jóságáról csak az annak iterálásával kapott szintetikus adatsorok vizsgálatával győződhetünk meg. Az iterálást a kiindulásként használt x(i) vektorok valamelyikével mint kezdeti értékkel kezdhetjük el. Sikertelen rekonstrukció esetén lehetséges, hogy a leképezés divergens minden kezdeti feltétel esetén, vagy éppen egy konstans érékhez (fixpont) konvergál. Amennyiben oszcilláló szintetikus adatsorokat kapunk, azok is lehetnek minőségükben eltérőek az analizált adatoktól, pl. határciklust kapunk. Mivel objektív kritérium nem létezik az iterált görbék jóságának megállapítására, az adatsorokat a lehető legtöbb eltérő transzformáció után hasonlítottuk össze: a fázistérbeli trajektóriákat, a Fourier-transzformáltakat, az idő-frekvencia-eloszlásokat és természetesen magukat az idősorokat. Hangsúlyozom, hogy egy az egyben nem hasonlítható össze a szintetikus adatsor a felhasznált változásokkal a kaotikus rendszerek kezdeti feltételekre vonatkozó érzékenysége miatt. Az itt leírtaktól eltérően a leképezést sokszor magán az adatsoron tesztelik. Ehhez az adatokat két részre osztják: az egyikre illesztik a leképezést (ez a tanító rész), a másikon pedig megjósolt és mért adatok közti eltéréssel definiálják a leképezés jóságát.
A rekonstrukció nem végezhető el tetszőleges beágyazási dimenzió (d) értékére. A célunk a legkisebb beágyazási dimenzió (dmin) meghatározása, ami elegendő a sikeres leképezés előállításához. A szükségesnél nagyobb beágyazási dimenzió használata nem célszerű, mivel az illesztendő paraméterek száma szükségtelenül megnövekszik. Matematikailag elég tág határ adható meg a minimális beágyazási dimenzió értékére: dmin > D, és dmin < 2D+1 , ahol D a vizsgált dinamikai rendszer valódi fizikai dimenziója. Több korábbi tanulmányban megkívánták, hogy dmin = 2D+1 legyen. Ez teljesen általános esetre garantálja, hogy a rekonstruált fázistérben ne legyenek egymást metsző trajektóriák, azonban a lehetséges adatsorok csak elhanyagolható hányadára kell a legszigorúbb megkötés szerint eljárni. Mivel D-t nem ismerjük, az előző egyenlőtlenségek számunkra fontos következménye, hogy dmin felső határt ad a rendszer dimenziójára.
A megfigyelt adatok csak ritkán olyan hosszúságúak, hogy pl. a kaotikus rendszereket jellemző fraktáldimenziót meghatározzuk. A leképezés itt is segítséget nyújt, hiszen segítségével tetszőleges hosszúságú szintetikus adatsorok hozhatók létre, s ezek kvantitatív jellemzői megadhatók. Az iterált fázistérbeli trajektória és a leképezés együttes ismerete lehetővé teszi az összes Ljapunov-exponens (Lambda i) meghatározását is. Ezek a mérőszámok adják meg a szomszédos trajektóriák divergenciájának értékét. Legalább egy pozitív exponensnek kell léteznie ahhoz, hogy kaotikus folyamat létrejöhessen, ezért a Ljapunov-exponensek ismerete egyértelmű kritériumot szolgáltat a káosz kimutatásához.
A csillagpulzáció kaotikus jelenségei
Az első kaotikus csillagmodellek másfél évtizede születtek (Buchler és Kovács 1987), s ezeket a jelenlegi modellszámítások sem tudták jelentősen továbbfejleszteni. Az egyedüli fejlődés az volt, hogy a turbulens konvekció figyelembevétele a pulzációs kódokban kitolta azt a periódusértéket, ahol a szabályos pulzáció kaotikussá válik. Ez a 20 nap körüli periódusérték jobban megközelíti a tapasztalati adatokat, de a hosszabb periódusú csillagok megfelelő modelljeinek elkészítése további kihívás.
A modellszámítások interpretálásában már születtek új eredmények az utóbbi időszakban is. A globális fázistér-rekonstrukció alkalmazásával azt kaptuk, hogy a W Virginis csillagmodellek kaotikus viselkedése egyértelműen megadható egy 3 dimenziós leképezéssel (Serre és munkatársai 1995). A leképezés Ljapunov-spektruma alapján a fraktáldimenzió egy 2,0-2,05 közötti érték, hasonlóan a Rössler-rendszerhez. Amikor az attraktor egy közel kétdimenziós felületen helyezkedik el, lehetőség van arra, hogy topológiai szempontból is jellemezzük az attraktort.
A topológiai analízis a periodikus pályák vizsgálatán alapul. Ha elegendő hosszúságú adatsor áll a rendelkezésünkre, akkor abban találhatunk közel periodikus pályákat. Az attraktor topológiája meghatározható abból, hogy a periodikus pályák miként járják be azt. Periodikus pálya alatt értek mindent, ami egzaktul ismétlődik valamekkora idő után. Ezek közül csak a legegyszerűbb az, amely egy hullámmal, egy közel szinuszos változással jellemezhető. A többi esetében néhány kissé eltérő "hullám" után ismétlődik megint a folyamat. A továbbiakban az ilyen pályákat, az ismétlődő sorozaton belüli nem tökéletes ciklusok száma szerint n-ciklusoknak nevezem. Egy adott topológia esetén nem létezhetnek tetszőleges n-ciklusok. A korlátozást az adja, hogy a fázistérben a pályák nem metszhetik egymást. Az attraktort ezen kívül összefüggőnek feltételezve - azaz elvileg bármelyik pontból eljuthatunk az attraktor bármelyik másik pontjába - további periodikus pályák lehetősége kizárható. Amennyiben tisztán kétdimenziós felületben gondolkozunk, egy periodikus pálya azt az előzőek alapján kettészelheti. A hengerpalásthoz hasonló topológia ezek alapján kapásból kiesik a számunkra érdekesek közül. Azt bármelyik egyszerű 1-ciklus kettévágja, bonyolultabb periodikus pályák pedig nem lehetnek, mivel önmagát metszené a trajektória.
A következő érdekes objektum a Möbius-szalag. Aki még nem tette meg, annak érdemes eljátszania vele. Csak egy darab papír, kis ragasztó és egy olló kell hozzá. Egy papírszalag két részét ragasszuk úgy össze, hogy ne hengerpalástot kapjunk, hanem legyen egy félfordulatnyi (180 fokos) csavarodás benne - ezzel létrehoztuk a Möbius-szalagot. Ha hosszában középen elvágjuk a szalagot, akkor ez nem esik két részre (mint egy hengerpalást esetében), hanem egy nagyobb kerületű gyűrűt kapunk, immár teljes csavarodással. A Möbius-szalagon tehát találtunk egy egyszerű periodikus pályát, ami még nem darabolja azt két részre. Mi a helyzet egy 2-ciklussal? A kísérlet ismét egyszerű: mielőtt összeragasztjuk a papirost, hosszában rajzoljunk rá két vonalat, amelyek éppen harmadolják a téglalapot. Összeragasztásnál az egyik vonal vége pontosan a másik vonal végéhez illeszkedik (igazából ehhez átlátszó fóliára kellene rajzolnunk, de a lap másik oldalára is behúzva az egyeneseket azonos eredményre jutunk). Íme, a papíron mindössze egy zárt vonalunk van, de ez egy 2-ciklusnak felel meg. Az ollóval a kézben ténylegesen tapasztalhatjuk, hogy egy vonal mentén el tudjuk vágni azt úgy, hogy az összes berajzolt vonalnál elhaladtunk. Az eredmény egy nagyobb és egy kisebb kerületű zárt szalag - azaz a 2-ciklus jelenléte esetén két diszjunkt részre esik szét egyszerű fázisterünk (az egyikből a másikba csak úgy juthatnánk el, ha metszenénk a 2-ciklust).
A Rössler-attraktor nagyon jó közelítéssel megadható két szalaggal. Ehhez két olyan papírcsíkra van szükségünk, amelyik az egyik végén kétszer olyan széles, mint a másikon. Az egyiket csavarodás nélkül illesztjük gyűrűvé, a másikat a Möbius-szalagnak megfelelően 180 fokos csavarodással. Az így létrehozott két alakzatot a csíkok végeinél egymáshoz illeszthetjük. Az együttes felületen a két szalag találkozási vonalánál az egyik irányból érkező pályák két lehetséges útvonalon, mehetnek tovább. Az egyes szalagokat jellemezhetjük a rajta lévő 180 fokos csavarodások számával, jelen esetben az egyiket 0-val a másikat 1-gyel. Egy "körbe-körbe" futó pályát így összességében topológiailag megadhatunk egy 1 és 0 karakterekből álló sorozattal. Hasonlóan a p-ciklushoz egy p-jegyű, 0 és 1 jelekből álló sorozat, a szimbolikus sorozat tartozik. A tisztán periodikus (1-ciklus) pálya vagy a "0" vagy az "1" egyelemű sorozat, de az előbbi (a korábbi megállapításunkhoz hasonlóan) nem megengedett pálya - itt figyelembe kell venni azt is, hogy csak egy irányba haladhatnak a pályák, s a hengerpalást két fele között csak az egyik irányba lenne lehetséges az átjárás, azaz az egyik oldalon csak egy tranziens idején tartózkodna a rendszer. Így a legegyszerűbb periodikus pálya csak az "1" lehet. A papíron rajzolgatva talán eljuthatunk néhány további periodikus pályához is, amelyek megfelelnek a kívánalmainknak, de ez már nem egyszerű feladat.
A jelen esetben ismertük a papír alakzatot, amit a továbbiakban templétnek hívok. A mérési, megfigyelési adatok feldolgozásakor egy pálya, vagy pályák ismeretében szeretnénk meghatározni a templétet. Egy kaotikus attraktor esetén a periodikus pályák instabilak, de nagyon sokáig követve egy kaotikus trajektóriát, az megközelítheti valamelyik n-ciklust. Nem kell mást tennünk, mint a megfigyelésekből kapott fázistérben keresni az időben távoli, de térben egymáshoz közeli pontokat. Amennyiben ismerjük a rendszerhez tartozó dinamikát (differenciálegyenleteket vagy leképezést), akkor iterációval egyértelműen meghatározhatók az instabil periodikus ciklusok. A következő kérdés, hogy miként azonosíthatjuk, hogy hány szalagból áll a templét, és azok közül éppen melyiken tartózkodik az attraktor. A periodikus pályák a Poincaré-metszeten mindössze néhány ponttal jellemezhetők (a határciklus egy ponttal, míg a p-ciklusok p darab ponttal). Minden egyes ponthoz megadható, hogy a szalagok közül melyiken található a Poincaré-metszet alapján gyártott első visszatérések térképe (Poincaré-leképezés) alapján.
Ha megtaláltuk az összes periodikus pályát és meghatározzuk a hozzájuk tartozó szimbolikus sorozatokat, akkor kvantitatív leírást kapunk az attraktorhoz. Kimutatták, hogy ez az információ elegendő lehet az attraktor topológiai jellemezéséhez. A teljes folyamat itt nem mutatható be, de pár lépést, kiindulópontot ismertetek. A szimbolikus sorozatokhoz található egy elv, amellyel sorba rendezhetők, illetve egy transzformáció, amellyel szimbolikus koordináták definiálhatók. Az adott attraktorban talált, a sorrendben a legmagasabb értékű pálya az összes, nála kisebb értékű periodikus pályát is indukálja. A két szimbolikus koordinátával definiált síkon a véges hosszúságú adatszegmensek egy-egy ponttal jellemezhetők, melyek között a periodikus pályák kitüntetett helyzetet foglalnak el. A szimbolikus síkon a periodikus pályák lehetséges hierarchiája jól jellemezhető. Síkra vetítve egy periodikus pályát a szalagok csavarodásai jellemezhetők azzal, hogy miként keresztezi saját magát a trajektória (a felül lévő milyen irányba halad). Erre egy algebrai módszer is használható, amivel egyszerűvé válik a topológiai szerkezet ellenőrzése.
A W Virginis-modell attraktora a Rössler-rendszerhez hasonlóan közel két szalaggal jellemezhető, de az egyes sávok finom, többrétegű szerkezete határozottabban megfigyelhető. Az előbbiekben ismertetett módon, a két szalaggal jellemzett topológia jól definiálja a rendszert. Az attraktoron az 10110 sorozattal jellemzett 5-ciklus indukálja a lehetséges periodikus pályákat. (A periodikus ciklusok szekvenciái 1, 10, 1011, 10111, 10110, 101110, 101111 stb.) A topológiára vonatkoztatva az az eredmény adódik, hogy az attraktor hasonló a Rössler-rendszerhez, de még egy csavarodás figyelhető meg az egyik szalagon (1. ábra).

1. ábra. A Rössler-rendszer (bal oldal) és a W Virginis-modell (jobb oldal)
attraktora. A templét a szaggatott vonal mentén összeillesztett két szalagból
áll
A modell vizsgálatánál kapott legfontosabb eredmény az, hogy attól függetlenül, hogy a csillag sugarát vagy annak teljes fényességét használtuk fel mint megfigyelt egydimenziós változót, azonos eredményhez jutottunk. A csillag dinamikájában a sugár alapvető változó, a luminozitás (teljes fényesség) viszont egy bonyolult leszármaztatott mennyiség. A Takens-tétel majdnem mindig alkalmazható, de lehetségesek a fizikai változók olyan függvényei, amelyeken keresztül vizsgálva a rendszert, torzított képhez jutunk. A topológiai azonosság alapján csillagok esetén a fényesség jól viselkedő mennyiség. Ez azért jelentős, mert a megfigyelések jelentős része csak a fényességet adja meg, csak elhanyagolható mennyiségben léteznek - a számunkra érdekes csillagok esetén - elegendő hosszúságú radiálissebesség-görbék.
Az RV Tauri típusú változócsillag, az R Scuti előzetes vizsgálata (l. Kolláth 1993), az adatsor Fourier-transzformációja és a geometriai fázistér-rekonstrukció kaotikus dinamika jelenlétére utalt. A globális fázistér-rekonstrukció újabb lehetőséget adott az előzetes eredmények megerősítésére és kvantitatív vizsgálathoz (Buchler és munkatársai 1995, 1996). Munkánkban az AAVSO (American Association of Variable Star Observers) vizuális megfigyelésekből származó adatbázisát használtuk fel. Az egyedi fényességbecslések hibája nagy (kb. 0,1 magnitúdó), de az adatpontok nagy száma miatt a 2-5 napos átlagok esetén már elfogadható a jel/zaj viszony. A rövid adathiányokat simító interpolációval fedtük le, ami egyúttal aluláteresztő szűrést is jelentett. Az általunk használt spline algoritmusban paraméterként megadható az eredeti adatok és a spline közötti négyzetes eltérés. A globális fázistér-rekonstrukciót a paraméter több értékére teszteltük, a 0,06 értéket találtuk optimálisnak, ami megfelel az adatsor zajszintjének. A legalacsonyabb beágyazási dimenzió, amely elvileg kaotikus folyamatot eredményezhet: d=3. Az R Scuti esetében azonban nem találtunk olyan 3 dimenziós leképezést, amelynek iterációjával a megfigyelésekhez közeli szintetikus adatsort kaptunk volna. Eggyel növelve a dimenziót viszont robusztus leképezés adódott. A változás jól modellezhető egy négydimenziós negyedrendű leképezéssel. A megfigyelt és az iterált adatsor egy-egy részét a 2. ábrán láthatjuk.

2. ábra. Az R Scuti megfigyelt fényváltozása (fönt) és az illesztett leképezés
alapján kapott szintetikus adatsor (lent)
A sikeres 4-dimenziós leképezés azt jelenti, hogy a fénygörbe leírásához elegendő négy közönséges differenciálegyenlet. A csillagpulzációra alkalmazva azt kapjuk, hogy mindössze két (komplex) pulzációs módus kölcsönhatása szükséges ahhoz, hogy az összetett és szabálytalannak tűnő változást modellezzük. Az illesztett leképezés alapján meghatároztuk a Ljapunov-exponenseket, melyekből egy pozitív, egy nullának tekinthető (folytonos áramlások esetén legalább egy Ljapunov-exponensnek zérónak kell lennie), a fennmaradó kettő negatív. Ez az első erős bizonyíték arra, hogy szabálytalan fénygörbe alacsony dimenziójú káosz eredménye. A Ljapunov-spektrum alapján becslést adhatunk a fraktáldimenzióra, melynek értéke az R Scuti esetén kb. 3,1. Ez azt jelenti, hogy a fázistér dimenziójának legalább 4-nek kell lennie.
A kapott leképezés lineáris stabilitásvizsgálata egy spirálisan növő és egy csökkenő amplitúdójú módust mutatott ki (instabil és stabil fókuszpont), amely a Shilnikov típusú instabilitásokra jellemző. A két módus frekvenciái közel vannak az 1:2 rezonanciához: f1 = 0,0069 nap-1 és f2 = 0,0147 nap-1. A kisebb frekvenciájú módus az instabil. Az ehhez tartozó mozgás növekvő amplitúdójú, kifelé spirálozó. Az amplitúdó növekedését a két módus kölcsönhatása állítja meg, azaz a mozgás átvált az f2 frekvenciájú befelé spirálozó mozgásba. A két rezgési módus kölcsönhatása megmagyarázza, miért négydimenziósnak adódott a rekonstruált rendszer, hiszen minden (komplex) rezgési módushoz két szabadsági fok tartozik. A megfigyelések értelmezésével kapcsolatban ez az eredmény azért jelentős, mert a 2f1 és az f2 közötti frekvenciatartományban a kölcsönhatásból eredő frekvenciamoduláció megfigyelhető lehet. Ilyen jellegű modulációt sem a megfigyelési zajok, sem a csillaghoz tartozó egyéb folyamatok (pl. konvekció, tömegvesztésből származó csillagkörüli anyag változó fényelnyelése) nem hozhatnak létre. Ezért az amplitúdó változásával korreláló frekvenciacsúszkálás a nemlineáris móduskölcsönhatás és az ebből származó kaotikusság lenyomata lehet. Félig szabályosan változó csillagok (RV Tauri, félszabályos és Mira típusú változók) tucatját vizsgáltuk meg az elmúlt évben idő-frekvencia-eljárások segítségével. Többségüknél megfigyelhető az említett moduláció. Az adatsor egyszerű Fourier-transzformációjával nem vehetők észre ezek a modulációk. Ennek fő oka, hogy ezeknél e frekvenciáknál az amplitúdó egyébként is kicsiny, s a periódus változása miatt még inkább elmosódnak ezek a komponensek. A Fourier-transzformált alapján sokszor tévesen szabályosan periodikusnak gondolják ezeket a csillagokat. Ha megfelelő idő-frekvencia-eloszlásokon alapuló módszerekkel vizsgáljuk az adatokat, s a magasabb frekvenciájú tartományt szűréssel felerősítjük, azonnal szembetűnő a valójában komplex viselkedés. Egyes csillagokról egymástól független megfigyelési adatok is rendelkezésre állnak: az egyik professzionális majd két évtizednyi fotoelektromos észlelési sorozat, a másik pedig amatőrcsillagászok fénybecslései alapján. A független és eltérő jellegű megfigyelési zajok ellenére a kapott idő-frekvencia-térképek szinte tökéletesen megegyeznek, azaz a módus-kölcsönhatások fényváltozásbeli lenyomatai szignifikánsak. Példaként az X Aurigae Choi-Williams típusú idő-frekvencia-eloszlását a 3. ábrán mutatjuk be. Jól megfigyelhető az első harmonikus környezetében az erős frekvenciamoduláció, amiről a Fourier-transzformált semmilyen információval nem szolgál.
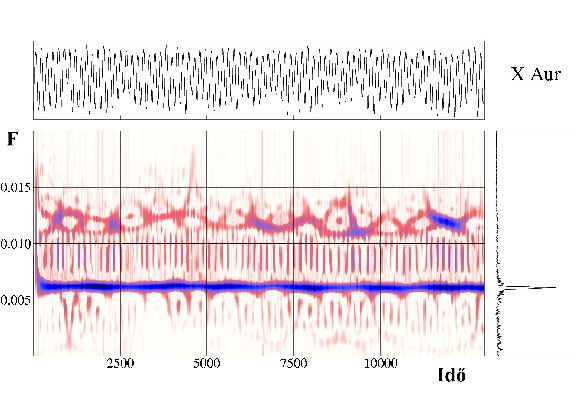
3. ábra. Egy Mira csillag, az X Aurigae fénygörbéje (fent), annak
Choi-Williams típusú idő-frekvencia-eloszlása (lent) és frekvenciaspektruma
(jobbra)
A naptevékenység kaotikus jellege
A naptevékenység változásai földi hatásokkal is járnak, például a globális klímaváltozásokban fontos szerepet játszhat a jelenség. Schwabe 1843-ban közölte a napfoltszámok 11 éves ciklusát, s mérföldkőnek számító munkájában már a maximumok nagyságának változására is bizonyítékkal szolgált. Ma már tudjuk, hogy a naptevékenység változása nagyon összetett jelenség, változó amplitúdóval és periódusokkal. A naptevékenység előre jelezhetősége régi probléma, és manapság is újabb és újabb kísérletek történnek a folyamat modellezésére.
A kaotikus folyamatok itt is fontos szerephez jutnak. Összefoglalónkban csak szemezgetünk az utóbbi években megjelent eredmények közül, amelyekben a nemlineáris dinamikai jelenségek és a naptevékenység kapcsolatával kapcsolatosak.
A napfoltok és más aktivitással kapcsolatos jelenségek változásának hátterében egy dinamó effektus van, amely a Nap differenciális rotációját kapcsolja a mágneses térhez. A dinamómodellek többsége mint nemlineáris dinamikai rendszer képes kaotikus folyamatokat produkálni. A dinamóelméletből leszármaztatott egyszerűsített modellek is jó kiindulópontot adnak a lehetséges kaotikus folyamatok tanulmányozásához. A redukált modellekről Charbonneau (2001) publikált összefoglalót. A dinamóegyenletek alapján több egydimenziós leképezés is felírható, lényegében a logisztikus leképezéshez közeli tulajdonságokkal. Ha a napfoltszám maximumainak adatsorából levonjuk annak megfelelően képzett mozgóátlagát, akkor egy olyan sorozatot kapunk, amelyben felváltva kisebb-nagyobb az érték. Az irodalomban páratlan-páros effektusként szerepel ez a folyamat. Ez hasonló a logisztikus leképezés esetén kapható perióduskétszereződési tartományhoz. A redukált dinamómodellekben is hasonló folyamatot figyelhetünk meg. A vizsgálatok szerint a páratlan-páros sorozat akkor is megmarad, ha a leképezést zajjal gerjesztjük. Ez fontos, mivel a Nap esetén jelentősek lehetnek magasabb dimenziójú (a konvekcióhoz kapcsolódó) folyamatok is. Vizsgáltak olyan sztochasztikus leképezést is, ahol e leképezés kontrollparamétere is véletlenszerűen változott, például mind epszilonn, mind gamman véletlen változó az alábbi egyenletben:
Pn+1 = gamman pn2 (1 - pn ) + epszilonn.
Ha (n értékeit a [4,5, 6,5] intervallumból választjuk, akkor ki-bekapcsoló típusú intermittencia jelensége is fellép, azaz a modell szerinti napfolttevékenységnek időszakonként csökken az intenzitása. Hosszan tartó minimumok valóban megfigyelhetők a napaktivitásban, de ezek jellege kissé eltérő.
Mit mondhatunk a megfigyelt napfoltszám váltakozása alapján a jelenség hátterében lévő dinamikáról? 150-200 évnyi megbízható adatsor áll a rendelkezésünkre, ami kevesebb, mint 20 ciklust jelent. Az adatsor rövidsége ellenére többen is megkíséreltek modelleket illeszteni az adatokhoz. Serre és Nesme-Ribes (1996) a már korábban bemutatott globális fázistér-rekonstrukciót alkalmazva azt kapta, hogy egy négydimenziós leképezéssel a megfigyelthez hasonló adatsorok készíthetők. A jelenségkör fontossága miatt módszerek széles skáláját alkalmazták már erre az adatsorra. Érdekes megközelítés a leképezés illesztése genetikai algoritmussal (Orfila és munkatársai 2002). Az eljárás lényege, hogy az időeltolás módszerével kapott állapotvektor véletlenszerűen kiválasztott elemeit a négy alapművelet közül véletlenül kiválasztott módon kapcsolják össze, s a lehetséges paramétereket az adatsor egyik részével illesztik. A kezdeti 120 populációból kiválasztják a legjobbakat az adatsor másik részén megfigyelt előrejelző képességük alapján. A megmaradt populáció elemeit véletlenszerűen keverik, és mutációkkal látják el, s a "természetes kiválasztódás" elölről kezdődhet. A 10 000 generáció után kapott egyenleteket fogadták el a naptevékenység modelljének. A saját kritikám az eljárásról az, hogy a kapott egyenlet alakja bevallottan nagyon esetleges. Kis változtatás az adatok kezdeti feldolgozásában (simítás, szűrés) merőben eltérő formájú eredményre vezethet. Ennek megfelelően a felírt formula nem mond semmit a folyamat hátterében lévő fizikai folyamatokról. Ne feledkezzünk el arról sem, hogy ezzel a módszerrel is csak a következő ciklusról mondhatunk valamit, s azt is meglehetősen nagy hibával.
Mivel még a közelmúltban is használtak lineáris sztochasztikus modelleket a napfoltszám változásának modellezésére, érdemes ellenőrizni, hogy ezek mennyire lehetnek elfogadhatóak. Sello (2001) ezt a kérdést is vizsgálta a napciklus előrejelzését tárgyaló munkájában. A szurrogátumok módszerét (olyan helyettesítő adatok, amelyek az adatsor valamely tulajdonságait utánozzák, jelen esetben a lineáris viselkedést) alkalmazta arra, hogy statisztikailag elenőrizze a lineáritás hipotézisét. A helyettesítő adatok a napfoltszám változásához illesztett lineáris sztochasztikus folyamatok voltak, amelyeket egy megfelelően választott lineáris és nemlineáris statisztika segítségével hasonlíthatók a megfigyelt adatokhoz. A nemlineáris statisztika olyan redundancia volt, amelyet az adatsor entrópiájából valamint az időeltolt idősorral kapott kereszt-entrópiájából származtattak. Ehhez a nemlineáris redundanciához természetes módon hozzárendelhető egy lineáris is. A vizsgálatok szerint a lineáris redundancia nem tesz különbséget a napfoltszám alakulása és s szurrogátumok között, de a nemlineáris redundancia egyértelműen mutatja ezen egyszerű modellek hiányosságait. Sello megadja a napfoltszámadatokból származtatott Ljapunov-exponenseket is, melyekből kettőt becsült pozitív értékűnek. A Ljapunov-dimenzió 4 felettinek adódik. Véleményem szerint egy ilyen rövid adatsorból túlzás egy ilyen értéket határozottan megadni, de az adatokban lévő komplexitás meggyőzően adódik a vizsgálatból. A munkájában az is egyértelművé vált, hogy a napfoltszám előrejelzéséhez nemlineáris modelleket kell használnunk, de a kaotikus viselkedés miatt a prognózisok erősen korlátozott jellegűek.
A változócsillagok esetén az idő-frekvencia-eloszlások finomszerkezete a káosz jellegzetességének bizonyult. A jelen sorok szerzője megvizsgálta a napfoltszám adatsorait is a frekvenciatartalom időbeli változása szempontjából. Itt is léteznek korábban nem regisztrált szerkezetek. Serre és Nesme-Ribes modelljeinek stabilitásvizsgálata is utal arra, hogy több rezgés kölcsönhatása is jelen lehet a háttérben lévő dinamikai rendszerben. Ha majd sikerül teljesen feltárni ezeket a központi csillagunkra vonatkozó fizikai jelenségeket, talán a szférák zenéjének a földi élet szempontjából legfontosabb hangszerét is megismerhetjük.
Irodalomjegyzék
Buchler, J. R., Kolláth, Z., Serre, T. and Mattei, J. A. (1996). Nonlinear Analysis of the Irregular Variable Star R Scuti. Astrophysical Journal 462, 489
Buchler, J. R. and Kovács G. (1987). Period-doubling Bifurcations and Chaos in W Virginis Models. Astrophysical Journal Letters 320, 57-62
Buchler, J. R., Serre, T., Kolláth, Z. and Mattei, J. A. (1995). A Chaotic Pulsating Star - The Case of R Scuti. Phys. Rev. Lett. 74, 842-845
Charbonneau, P. (2000). Multiperiodicity, Chaos and Intermittency in a Reduced Model of the Solar Cycle. Solar Physics 199, 385-404
Kolláth Z. (1993). Égi káosz. Magyar Tudomány 38, 415-424.
Letellier, C., Gousbet, G., Soufi, F., Buchler, J. R. and Kolláth, Z. (1996). Chaos in Variable Stars: Topological Analysis of W Vir Model Pulsations. Chaos 6(3), 466-476
Orfila, A., Ballester, J. L., Oliver, R., Alvarez, A. and Tintoré, J. (2002). Forecasting the Solar Cycle with Genetic Algorithms. Astronomy and Astrophysics 386, 313-318
Sándor Zs., Érdi, B. and Efthymiopoulos, C. (2000). Celest. Mech. and Dyn. Astron. 78, 113
Sello, D. (2001). Solar Cycle Forecasting: A Nonlinear Dynamics Approach. Astronomy and Astrophysics 377, 312-320
Serre, T., Buchler, J. R. and Kolláth, Z. (1996). Search for Low Dimensional Chaos in Variable Star Data. Astronomy and Astrophysics 311, 833-851
Serre, T. and Nesme-Ribes, E. (2000), Nonlinear Analysis of Solar Cycles. Astronomy and Astrophysics 360, 319-330