Magyar Tudomány, 2004/1 59. o.

Ökológia

Scheuring István

a biológiai tudományok kandidátusa, ELTE Növényrendszertani és Ökológiai Tanszék, MTA Ökológiai és Elméleti Biológiai Kutatócsoport

Matematikai modellek az ökológiában

Bevezetés

A XX. század első évtizedei a modern fizika kialakulásának időszaka. Gyaníthatóan kevesebben tudják, hogy e csodálatos felfedezések árnyékában, ezidőtájt rakták le a matematikai ökológia alapjait is. Míg a huszadik század kiemelkedő elméleti fizikusait minden természettudós ismeri, addig az elméleti ökológia megalapozóiról csak a szakmabeliek hallottak. Emlékezzünk meg tehát néhány mondatban a nagy elődök munkájáról. Érdekes, hogy többségük (pl. Sir Ronald Ross, William R. Thompson, Vito Volterra) valamilyen konkrét gyakorlati probléma megoldásához alkalmaztak matematikai modelleket. Az általános elméleti kérdésekre koncentráló Alfred J. Lotka inkább kivételnek számított.

A hőskor

Ronald Ross, foglalkozására nézve orvos, sokoldalú tehetséggel megáldott ember volt. Kifejezett érzéke volt a matematikához, de festett, verseket és színdarabokat is írt. Orvosként Indiában dolgozott, ahol a malária-fertőzés ökológiai hátterével foglalkozott. Felismerte, hogy a betegség terjedésének jellemzői a malária kórokozó, a közvetítő szúnyog és az ember közti kapcsolat matematikai modelljének segítségével jól magyarázhatók. Dinamikai modelljének segítségével megmutatta, hogy a betegség csak a terjesztő szúnyogok egy kritikus denzitása felett marad fenn tartósan, tehát a legjobb védekezés a szúnyogok irtása. A maláriafertőzés biológiai ökológiai hátterét felfedő kutatásait 1902-ben Nobel-díjjal jutalmazták.

Vito Volterra a matematikai fizika neves professzora volt Rómában. Figyelmét ökológiai problémák felé későbbi veje, a biológus Umberto D'Ancona fordította. D'Ancona az Adriai-tenger halászati adatait elemezve észrevette, hogy az I. világháború idején, amikor az aknazár miatt a halászat jelentősen visszaesett, egyes ragadozó halak fogási aránya megnőtt, míg a ragadozók potenciális zsákmányainak számító halfajok egyedszáma visszaesett. Kimutatta továbbá, hogy mind a ragadozó, mind a zsákmány halak populációinak mérete egymást követve ciklikusan változik. Vajon miért van ez így? - kérdezte az ifjú biológus apósától. Volterra mint igazi fizikus a probléma lehető legegyszerűbb matematikai modelljét vizsgálta: egyetlen ragadozó és egyetlen zsákmány faj denzitásának változását egy kétváltozós közönséges differenciál-egyenletrendszerrel írta le. Modellje segítségével könnyen magyarázni tudta veje megfigyeléseit. Eredményeit 1926-ban publikálta olasz nyelven. E cikkről a Nature rövid ismertetőt közölt. Érdekes módon egy másik fizikusnak, az amerikai Alfred J. Lotkának, egy évvel korábban könyve jelent meg A fizikai biológia elemei (Elements of Physical Biology) címen, melyben Volterra eredményei lényegében mind megtalálhatóak voltak. Ez a felismerés az egyébként elég nehéz körülmények között és szakmai izoláltságban élő Lotkát meglehetősen felkavarta. Ráadásul könyvének célkitűzése, az ökológiai kapcsolatok matematikai leírása, sokkal általánosabb volt, mint Volterra idézett cikkének motivációja. Bár a két tudós viszonya a prioritási viták miatt később sem volt felhőtlen, a köztük lévő verseny és tehetségük eredményeként kiemelkedő szerepük volt a matematikai ökológia megteremtésében. Egyikük egy konkrét problémán keresztül jutott el a legáltalánosabb elméleti kérdések matematikai megfogalmazásáig, másikuk alapvetően ezzel a szándékkal kezdett az ökológiával foglalkozni.

Az ökológiai modellek jellemzői

A többi természettudományos diszciplínához hasonlóan a matematika szerepe az ökológiában a téridő folyamatok tömör leírása, a mintázatok mögött húzódó mechanizmusok felderítése. Azonban a fizikai vagy a kémiai rendszerekkel összehasonlítva az ökológiai rendszerek lényegesen összetettebbek. Egy populáció egyedei különböznek egymástól életkorban, öröklődő és szerzett tulajdonságokban, továbbá az élettelen környezet legtöbbször térben és időben is nagymértékben heterogén. Egy élőközösségben számos, sokszor több száz különböző populáció egyedei vannak egymással kölcsönhatásban, s ezek a kapcsolatok jellemzően nemlineárisak és sztochasztikusak. Ráadásul, ami fontos lehet például egy vízi élőközösségben, az egyáltalán nem lényeges mondjuk egy gyeptársulásban vagy egy erdőben. Míg például egy gyeptársulás kialakításában döntő szerepe van a térbeli kényszereknek, addig a planktonközösségekre inkább az áramló víz fizikai tulajdonságai vannak nagy hatással. Maga a vizsgálat tárgya rendkívül diverz és komplex, felépítése alapvetően hierarchikus.¹ Ebből következik, hogy a rendszereket leíró matematikai modellek is nagyon sokfélék és bonyolultak. Igen ám, de ezekből a nagyon részletes, sokparaméteres és sokváltozós matematikai modellekből általános következtetéseket aligha lehet levonni. Ezt a problémát felismerve, az elméleti ökológusok kutatásaik során két irányt követnek. Az első irányzat (hasonlóan Lotkához és Volterrához) igyekszik minél egyszerűbb, a folyamat lényegét megragadó ún. stratégiai modellek segítségével minél szélesebb körben érvényes megállapításokat tenni, a második csoport egy-egy működésében jobban ismert rendszert igyekszik minél pontosabban leírni ún. részletes modellekkel (ahogy egykor Ross is tette). Az első csoport inkább alap-, a második inkább alkalmazott kutatásokkal foglalkozik.

Természetesen a fizikai vagy kémiai modellekhez hasonlóan az ökológiai modellek is alapvető posztulátumok alapján építik fel a konkrét modelleket. A legfontosabb azt leszögezni, hogy az ökológiai kutatások alapegysége a populáció, bár sokszor érdemes (és érdekes) a populációnál magasabb szerveződési szintű egységek (élőközösségek, társulások, biomok) dinamikai viselkedését vizsgálni. Mivel a populációkról és az azokat felépítő egyedekről többet tudunk, mint a magasabb szerveződési egységekről, általános érvényű posztulátumokat a populációkra lehet megfogalmazni. Az egyik legfontosabb kiinduló posztulátum, hogy ha a környezeti hatásokban nincsenek szisztematikus változások, akkor a populáció egyedszáma exponenciálisan változik. Ez egyszerűen azért van, mert ebben az esetben a populáció egyedszámváltozását (az időátlagban) állandó születési és halálozási ráták határozzák meg. Ez a megállapítás analóg a newtoni tehetetlenség törvényével: egy teljesen ideális esetben, melyet igazából csak gondolatkísérlet útján tudunk előállítani, meg tudjuk mondani a test, illetve a populáció dinamikai viselkedését. Természetesen az exponenciális növekedés, illetve csökkenés elvét a megfigyelések és a kísérletek nagyon jó közelítéssel igazolják. Egy táptalajban gazdag baktériumtelepen a populációméret kezdetben exponenciálisan növekszik, ilyen a betegségszám növekedése minden járvány kitörésekor is.

Ezek után azokat a posztulátumokat érdemes lefektetni, melyek segítségével a valós populációk dinamikai viselkedését leírhatjuk. Ilyen posztulátum például, hogy minden populációban van egy felső határa a denzitásnak, amelyet a populáció nem léphet túl. Mivel a rendelkezésre álló források végesek, ez a józan ésszel teljes összhangban lévő megállapítás. Kimondva-kimondatlanul ezt a feltevést használjuk, amikor a populációnövekedés denzitásfüggését matematikai modellekben alkalmazzuk. Például a szaporodáshoz tápanyagfelvételre van szükség, és a szaporodási sebesség ennek a tápanyagfelvételnek monoton növő függvénye. A tápanyagfelvétellel kapcsolatban két további általános összefüggést vagy posztulátumot mondhatunk ki: 1.) alacsony tápanyag-denzitás esetén a tápanyagfelvétel arányos a forrás denzitásával, 2.) magas tápanyag-denzitás esetén a fogyasztó fiziológiai képességei felső határt szabnak a tápanyagbevitelre, s így a szaporodási sebességre is. E két utóbbi posztulátumon alapulnak a speciális esetekre megfogalmazott úgynevezett funkcionális válaszfüggvények, azaz azok a függvények, melyek a tápanyagmennyiség és az egységnyi idő alatt felvett tápanyag között teremtenek kapcsolatot (Turchin, 2003). Bármilyen jellegű matematikai modelljét vizsgáljuk a populációknak, illetve a populációk alkotta közösségeknek, társulásoknak, ezeknek a posztulátumoknak eleget kell tenni.

Egy tudomány akkor fejlődik egészségesen, ha a kísérleti (terepi, laboratóriumi) és az elméleti (matematikai modelleken alapuló) kutatások ismerik és alkalmazzák egymás eredményeit. Sajnos az ökológiában ezen a lényeges ponton komoly nehézségek vannak, elsősorban azért, mert az ökológiai folyamatok többsége olyan lassú és a rendszerek olyan összetettek, hogy a kísérletezés és a terepi megfigyelések is komoly akadályokba ütköznek. Világszínvonalú terepökológiához hosszú időre, átgondolt kutatási stratégiákra és sok pénzre van szükség. Annak ellenére, hogy ma már sok helyen végeznek gondosan tervezett, hosszú távú ökológiai kísérleteket az elméleti ökológusok sokszor nem tehetnek mást, mint igyekeznek a meglévő adatokat összegyűjteni, elemezni, és ezek alapján a modellek jóslatait a terepi eredményekkel összevetni, továbbá a stratégiai modellek viselkedéséből viszonylag általános érvényű hipotéziseket megfogalmazni. A következő fejezetben néhány, a matematikai modellek támogatásával kialakított hipotézisről, illetve egy-egy olyan kutatási területről kívánok szólni, ahol a kísérleti és terepadatok matematikai modellek együttes alkalmazása vezetett új eredményekre.

Modellek, hipotézisek, ellentmondások

A modellezés egyik legfontosabb erénye, hogy a modellek alapján egyértelműen megfogalmazott feltételek mellett határozott, sokszor nagyon éles következtetéseket lehet megfogalmazni. Ilyen például a kompetitív kizáródás elve. A tápanyagforrások és a fogyasztók dinamikáját közönséges differenciálegyenletekkel leírva arra a megállapításra jutunk, hogy a stabilan egyensúlyban lévő fajok száma nem haladhatja meg a független források számát. E matematikai eredmény legizgalmasabb vonása, hogy a terepi megfigyelések egyáltalán nem támasztják alá. George Evelyn Hutchinson, az elmúlt század egyik legnagyobb ökológusa, már a negyvenes években felfigyelt arra, hogy az együtt élő fajok száma a legtöbb élőközösségben messze túlhaladja a limitáló források számát. Az elmélet és a valóság közötti ellentmondás, mint oly gyakran, rendkívül termékenyen hatott a tudomány fejlődésére. Azóta számtalan matematikai modell és terepi megfigyelés eredményeként sokkal összetettebben látjuk ezt a kérdéskört; kiderült, hogy az adott élőközösségtől függően igen sokféle, a fajok együttélését fenntartó mechanizmus képzelhető el. Például, ha a tápanyagforrások vagy (belső dinamikai okok miatt) a populációdenzitások fluktuálnak, esetleg az élőlények túlélése külső hatások miatt időnként lecsökken, akkor a tartósan együtt élő fajok száma meghaladhatja a független források számát. Matematikai modellek segítségével sikerült kimutatni azt is, hogy a fitoplankton élőközösségekben az áramló víz kaotikus keveredése² is hozzájárulhat a versengő fajok együttéléséhez. Annak következtében, hogy a keveredés hatására a tápanyagforrás és a fogyasztók is egy fraktál mentén mozognak, a tápanyagfelvétel a kis denzitású fogyasztó számára rendkívül hatékony lesz. Ennek következtében a kevésbé hatékony kompetitor gyorsabban fog szaporodni, mint a hatékonyabbak, ha elég kis denzitásban van jelen (például Károlyi et al., 2000; Scheuring et al., 2003). A fitoplankton esetében a herbivóroknak (a fitplonktont fogyasztó zooplankton) az élőközösség szabályozásában általában nincs jelentős szerepe, de számos más közösségben maga ragadozó vagy valamilyen parazita az, aki a versengő fajokat egyensúlyban tartja, növelve ezzel a közösség fajgazdagságát. Ezen a ponton átléphetünk egy másik szövevényes területre: a táplálékhálózatok témakörébe.

Miközben a fajok kapcsolatát elsősorban a forrásokért való versengésként fogtuk fel, elhallgattuk azt a nyilvánvaló tényt, hogy heterotróf fogyasztók esetén a források maguk is élőlények. Egy-egy élőközösség akár több száz fajból álló táplálkozási hálózatot alkot. Számos, távlatilag "életbevágóan fontos" kérdés tehető fel a táplálékhálózatokkal kapcsolatban: Milyen topológiai és dinamikai tulajdonságokkal rendelkeznek ezek a hálózatok, vannak-e általános érvényű jellegzetességeik? Hogyan épülnek föl és mennyire stabilak a külső zavarokkal szemben? Robert May korszakalkotó könyvében (May, 1974) az ilyen általános problémák megközelítéséhez használt stratégiai modellek segítségével számos kiindulópontként használható megállapítást tett. Kimutatta például, hogy a táplálékhálózat komplexitásának növelésével a modellezett hálózat stabilitása csökken. Akárcsak a kompetitív kizáródás elve esetén ez a következtetés sincs igazán összhangban a terepi megfigyelésekkel. Tehát a modellek lényeges ponton élnek túlzott egyszerűsítésekkel. A valósághoz jobban közelítő matematikai modellek vizsgálatának eredményeként néhány éve arra hívták fel a figyelmet, hogy a táplálékhálózatban lévő néhány gyenge kölcsönhatás³ jelentősen fokozhatja a hálózat stabilitását (McCann - Hastings, 1997; McCann et al., 1998). Bár e sorok írója saját kutatásai alapján kételkedik az iménti megállapítások általánosságában, íme egy újabb elméleti eredmény, melynek jelentős szemléletformáló ereje volt az utóbbi években.

Eddig olyan kutatásokról tettünk említést, ahol a modellezés meglepő, a megfigyelésekkel ellentmondó eredményei sarkalták mind az elméleti, mind a terepbiológusokat az adott kérdéskör mélyreható tanulmányozására. Vannak esetek, amikor a rendelkezésre álló adatok elemzése a modellezési ismeretekkel társulva hoznak létre érdekes felfedezéseket. Az ökológiai rendszerekre jellemző nemlineáris kölcsönhatások eredményeként a populációk denzitása gyakran ciklikusan változik. Matematikai modellek segítségével megmutatható, hogy ha a populáció növekedését nem az aktuális táplálékmennyiség határozza meg, hanem a populáció demográfiai szerkezete, akkor a ciklus periódusa rövidebb lesz, mint olyan populációknál, ahol a növekedést egy forrás limitálja. Ezt az eredményt és a meglévő terepi adatokat felhasználva nemrégiben kimutatták, hogy a generalista (sok független forrást kiaknázni képes) fajok dinamikai szempontból úgy viselkednek, mintha egyetlen, a táplálékhálózatból kiemelt fajt vizsgálnánk, a specialisták viszont hosszabb periódussal fluktuálnak. Tehát a generalisták csak gyengén csatolódnak a táplálékhálózatba, ezzel szemben a specialisták a forrásokhoz erősen csatolódva alkotnak rendszert (Murdoch et al., 2002). Lehet, hogy ennek alapján a nagyméretű táplálékhálózatok elemzése is egyszerűbbé válik? Vajon szélesebb adatbázist figyelembe véve, illetve nem-ciklikus esetekben is lehet-e hasonló megkülönböztetést tenni a generalisták és a specialisták között? Ezek egyelőre nyitott kérdések, de biztos vagyok benne, hogy nem kell sokáig várni a válaszokra.

Modellek és adatok

Ahogy a gyümölcsmuslica a genetikusok egyik kedvelt kísérleti élőlénye, úgy az elméleti ökológusoknak is vannak kedvelt kísérleti rendszereik. Fontos, hogy a vizsgálandó közösség kevés fajból álljon, könnyű legyen azokat laboratóriumi körülmények között tartani, és rövidek legyenek a generációs idők. Ilyen szempontból ideálisak a planktonközösségek és bizonyos rovarok is. (Például a fitoplankton-zooplankton közösségekben a plankton denzitások ciklikusságát az akvárium színének ciklikus változása azonnal jelzi.) Az egyik legnépszerűbb laboratóriumi rovar a Tribolium castaneum (lisztbogár). Egy amerikai csoport lassan egy évtizede tart ilyen rovarokat ellenőrzött körülmények között. Folyamatosan mérik a populáció demográfiai adatait, és nagyon átgondolt modellépítéssel próbálják a populáció dinamikáját minél pontosabban leírni (Dennis et al., 2001). Részletes, de mégsem túlzottan bonyolult modelljük nagyon szépen illeszkedik a mérésekhez. Ráadásul, a modell jóslataival teljes összhangban, az imágók halálozási rátájának változtatásával igen sokféle dinamikai viselkedést elő lehetett idézni. Például, nagyon nagy halálozási ráták esetén a populáció egyedszáma kaotikusan változik.

Az elméleti ökológusokat a hetvenes évek eleje óta intenzíven érdekli, hogy az ökológiai rendszerekben mennyire jellemző a kaotikus viselkedés. Bár a populációdinamikai, ökológiai modellek sokaságában mutatták ki a káosz jelenlétét bizonyos paramétertartományokban, a lisztbogár talán az egyetlen meggyőző kísérleti bizonyíték arra, hogy (legalábbis mesterséges körülmények között) a káosz a populációk lehetséges dinamikai állapota. A meglévő számos, de igen rövid populációs adatsor viszont nem igazán alkalmas e kérdés megválaszolására. Arról nem is beszélve, hogy sokváltozós, zajos dinamikai rendszerekben alacsonydimenziós determinisztikus káoszról⁴ beszélni értelmetlen. Ezért az adatsorokból újabban inkább azt próbálják meg kideríteni, hogy a mögötte lévő dinamikai rendszer mennyire érzékeny a zajra, milyen erős a rendszerben periodicitás stb. (Turchin, 2003). Ezek a kutatások felhívják a figyelmet arra, hogy még a legegyszerűbb stratégiai modelleknek is figyelembe kell venniük, hogy az ökológiában jellemzően nemlineáris kapcsolatok vannak, ahol a külső és belső hatások zajos jellege nem elhanyagolható.

Folytonos leromlás, növekvő fluktuációk, hirtelen katasztrófák

Az átlagos éves középhőmérséklet, a szén-dioxid-koncentráció növekedése, a talaj pH-jának csökkenése, a természetes élőhelyek feldarabolódása egyaránt az emberi hatások okozta folyamatok. De a természetes szukcesszió hatására is lassú folytonos változások mennek végbe a mikroklímában és a biotikus feltételekben is. Vajon ezek a változások hasonlóan lassú és megjósolható deformációkat okoznak az ökológiai rendszerekben, vagy eredményezhetnek igen gyors katasztrofális változásokat is? A kérdés korántsem akadémikus, de a megalapozott válaszhoz szükség van a modellezők stratégiai modelljeire. Az imént hangsúlyozott nemlineáris kölcsönhatások miatt könnyen előfordulhat, hogy egy ökológiai rendszernek több alternatív stabil egyensúlyi állapota van. Megfigyelhető ez a jelenség például egy olyan ökológiai rendszer matematikai modelljében, ahol valamilyen rovar fogyasztja egy erdő lombját, és a rovarokat egy állandó egyedszámú, aktív keresőképpel rendelkező ragadozó fogyasztja. A lombkorona biomasszája a lassan változó paraméter a modellben. Az 1. a ábra egy ilyen rendszer stabil és instabil állapotait mutatja be valamilyen lassan változó külső paraméter függvényében. Látható, hogy egy adott paramétertartományban a rendszernek két stabil egyensúlyi állapota is lehet. E két állapot vonzó tartományát egy instabil állapot választja el egymástól (szaggatott vonal). A paraméter növelésével az ökológiai állapot folytonosan változik, mígnem elérkezünk a B1 bifurkációs ponthoz, ahol hirtelen ugrik át a másik stabil állapotba. Érdemes hangsúlyozni, hogy semmi sem jelzi előre azt, hogy a rendszer közeledik a bifurkációs ponthoz! Viszont, ha vissza szeretnénk vezetni a rendszert az eredeti állapotba, akkor a környezeti változó értékét csökkenteni kell, egészen addig, míg a B2 pontba jutunk. A rendszerben hiszterézis van, azaz az eredeti állapot visszaállításához nem elégséges, ha környezeti paramétereket az eredeti szintre állítjuk vissza. A bifurkációs pont felé közeledve a stabil állapot vonzó tartománya egyre szűkül, tehát a természetes fluktuációk az ökológiai rendszerben egyre nagyobb eséllyel okozhatnak drámai változásokat. A rendszer a másik stabil állapotba ugrik át, ha az ökológiai állapot annyira fluktuál, hogy az instabil állapoton átjutva a másik stabil állapot vonzáskörébe jut (1. b ábra, F1 pont). Nemcsak a folytonos környezeti változások, hanem a megváltozott viszonyok miatt megnövekedett fluktuációk is okozhatnak katasztrofális változásokat (1. b ábra, F2 pont). Természetesen ezek csupán a matematikai modellekből származó megállapítások, de a megfigyelések alátámasztják őket. A már említett erdő-rovar-rovarevő rendszerben közismert példák vannak arra, hogy a lombozat növekedésével a rovarok egyedszáma lassan, majd egy kritikus értéket elérve ugrásszerűen növekszik (gradáció). A gradációt a tápnövény letarolása miatt egyedszámcsökkenés követi, és a ciklus kezdődik elölről. Több sekély tóban az eutrofizáció is gyaníthatóan hasonló jelenség. Ha a bevitt tápanyagmennyiség elér egy kritikus értéket, a tóban hirtelen szaporodnak el bizonyos algák, vagy a hínárállomány tömege növekszik ugrásszerűen (ez persze csak az 1-2 méter mély tavakban fordul elő). Ettől a tó mélyebb részére nem jut el elég napfény. Ezért az ott élő fotoszintetizáló élőlények többsége kipusztulhat, majd az őket fogyasztó állatok is eltűnhetnek a tóból. Az eredetihez hasonló fajkészletű állapot visszaállításához gyakran a kritikus értéknél jóval alacsonyabb tápanyagbevitelre van szükség (Scheffer et al., 2001). Tehát a hiszterézis egyértelműen megfigyelhető.

Összefoglalás

A természettudományok a matematika nyelvén íródnak. Természetesen az ökológia ebből a szempontból sem kivétel, bár a folyamatok matematikai modellezése egyelőre szerényebb sikereket képes felmutatni, mint az élettelen természettudományok. Véleményem szerint ennek legalább három oka van: egyrészt a vizsgálat tárgya rendkívül összetett, másrészt a kísérletezés és terepi adatgyűjtés is számos nehézségbe ütközik, harmadrészt ez a tudományterület rengeteg új matematikai módszer kifejlesztését is igényli.

A nehézségek ellenére a fejlett statisztikai eljárások mellet a matematikai modellalkotás alapvető és egyre nagyobb fontosságú részét képezi a biológiának és ezen belül az ökológiai kutatásoknak is. Természetesen hazánkban is vannak kutatók, akik kifejezetten ökológiai modellezéssel foglalkoznak. Ilyen jellegű kutatások elsősorban, az ELTE Növényrendszertani és Ökológiai Tanszékén, a Genetika Tanszékén, a Fizikai Biológia Tanszékén, a Vácrátóti Botanikai Intézetben és a KLTE Ökológia Tanszékén folynak. Bár csupán tucatnyi szakemberről van szó, túlzás nélkül állítható, hogy a magyar elméleti ökológiai iskola eredményeivel nevet szerzett a tudományos világban. A sikerek hátterében egyértelműen ott található néhai Juhász-Nagy Pál (pl. Juhász-Nagy, 1986), akinek szellemi hagyatéka és személyes varázsa máig érezhetően éltető ereje az ökológiai modellezőknek.

Köszönetnyilvánítás

A szerzőt az OTKA 032423-as és a 037726-os számú pályázata, valamint a Bolyai János kutatói ösztöndíj támogatja. Köszönöm Bartha Sándor, Jordán Ferenc és Pásztor Erzsébet kritikai észrevételeit, javaslatait.

Kulcsszavak: komplexitás, nemlineáris dinamika, populáció, sztochasztikus folyamatok

1 Az egyedek populációkat, a populációk ismétlődően tartósan együtt előforduló populáció-kollektívumokat alkotnak.

2 Kaotikus keveredés esetén a vízben mozgó részecskék pályája kaotikus, bár a sebességtér az idő folytonosan változó függvénye (ellentétben a turbulens áramlásokkal). A keveredés erős, de nem tökéletes.

3 Két faj akkor van trofikus kölcsönhatásban, ha az egyik fogyasztja a másikat. Annak erősségét leggyakrabban az egységnyi idő alatt felvett és leadott biomassza mennyiségével szokták definiálni. A hatás akkor tekinthető gyengének, ha az adott populáció többi trofikus kölcsönhatásánál sokkal kisebb.

4 A káosz kifejezést olyan teljesen determinisztikus rendszerekben megfigyelhető szabálytalan mozgásra alkalmazzák, ahol a független változók száma (azaz a rendszer dimenziója) nem több, mint hat vagy mondjuk tizenkettő.

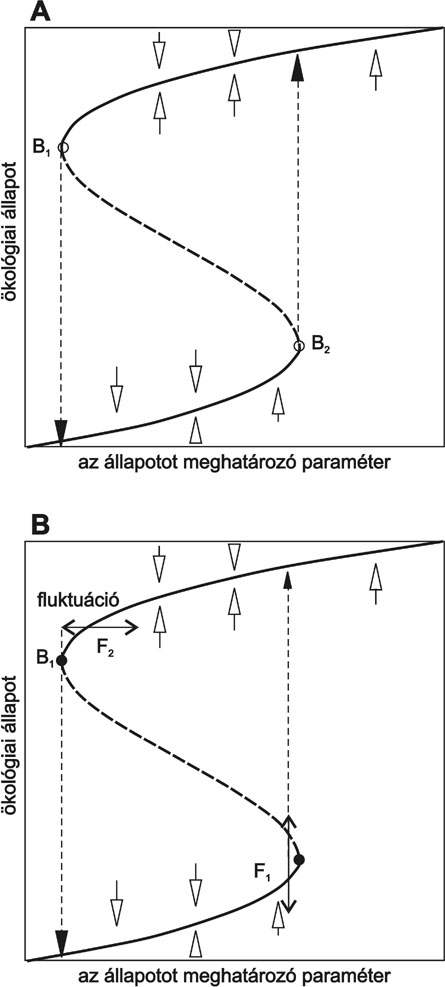1. ábra * Az egyensúlyi állapotok az ökológiai rendszer valamilyen paraméterének függvényében. A stabil állapotokat folytonos, az instabilt szaggatott vonallal jelöltük. a) Ha a paraméter változása során a rendszer eléri a B1 (B2) bifurkációs pontot, akkor az átugrik a másik stabil állapotba. b) A bifurkációs pont közelében, az ökológiai állapot fluktuációjának hatására (F1), a két stabil állapotot elválasztó instabil állapotot átlépve jut el a rendszer az alternatív stabil állapotba. Az állapotot meghatározó paraméterek megnövekedett fluktuációja (F2) is vezethet bifurkációhoz.

IRODALOM

Dennis, Brian - Desharnais, R. - Cushing, J. M. - Henson, S. M. - Costantino, R. F. (2001). Estimating Chaos and Complex Dynamics in an Insect Population. Ecological Monographs. 71, 277-303

Juhász-Nagy Pál (1986). Egy operatív ökológia hiánya, szükségszerűsége és feladatai. Akadémiai, Budapest

Kingsland, Sharon E. (1995). Modelling Nature. The University of Chicago Press, Chicago

Károlyi György - Péntek Á. - Scheuring I. - Tél T. - Toroczkai Z. (2000). Open Chaotic Flow: The Physiscs of Species Coexsitence. Proceedings of the National Academy of Sciences of the USA. 97, 13661-13665

May, Robert M. (1994). Stability And Complexity in Model Ecosystems. Princeton University Press, Princeton, USA (Second Edition)

McCann, Kevin - Hastings, Alan (1997). Re-Evaluating the Omnivory-Stability Relationship in Food Webs. Proceedings of the Royal Society of London. Series B. 264, 1249-1254

McCann, Kevin - Hastings, Alan - Huxel, Gary R. (1998). Weak Trophic Interactions and the Balance of Nature. Nature. 395, 794-798

Murdoch, William W.- Kendall, B. E. - Nisbet, R. M. - Briggs, C. J. - Mccauley, E. - Bolser, R. (2002). Single-Species Models for Many Species Food Webs. Nature. 417, 541-543

Scheffer, Marten - Carpenter, S. - Foley, J. A. - Folke, C. - Walker, B. (2001). Catastrophic Shifts in Ecosystems. Nature. 413, 591-596

Scheuring István - Károlyi Gy. - Tél T. - Torockai Z. (2003). Competing Populations in Flows with Chaotic Mixing. Theoretical Population Biology. 6, 77-90

Turchin Peter (2003). Complex Population Dynamics: A Theoretical/Empirical Synthesis. Princetone University Press, Princeton