Útban az óriásmolekulák felé: „lineárisan skálázódó” elméleti kémiai módszerek Surján Péter az MTA doktora, Eötvös Loránd Tudományegyetem Kémiai Intézet Elméleti Kémia Tanszék
surjan @ chem.elte.hu
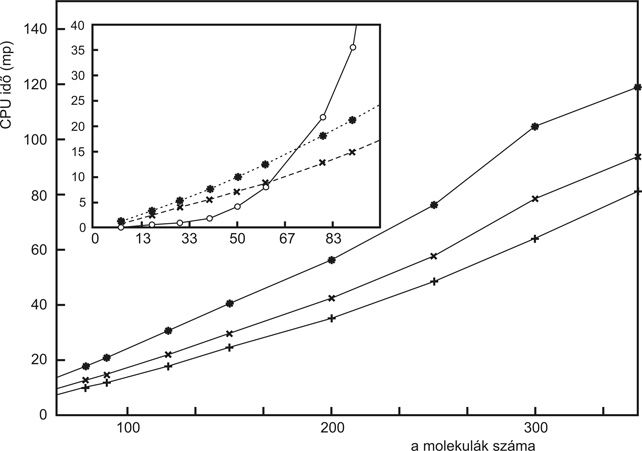
Az elméleti kémia legújabb eredményei lehetővé tehetik, hogy hamarosan a soha nem álmodott méretű molekulák szerkezete puszta számítások révén is felderíthető legyen. Szenvedélyesebben szólva: a szemünk láttára épül egy híd a tudományban a fizikától a kémián át az anyagtudományig és a molekuláris biológiáig. Az igazán bonyolult anyagi rendszerek, amelyekkel az anyagtudományban, a makromolekulák világában vagy éppenséggel a biológiában találkozunk, nem érthetők meg kizárólag kísérleti és műszeres technikák alkalmazásával. Az empirikus eredmények értelmezéséhez és kiegészítéséhez megbízható számításokra lenne szükség, ezek azonban nagy rendszerekre bajosan kivitelezhetőek. Szent-Györgyi Albert mesélte egy interjúban, hogy egyszer fizikusokhoz fordult egy molekuláris biológiai jellegű kérdéssel. Amikor a fizikusok megtudták, hogy az őt érdeklő rendszerben kettőnél több elektron van, reménytelennek nyilvánították a probléma megoldását. Ez a XX. század közepén történhetett, és a szigorú fizikai elveken alapuló elméleti kémia hatalmas utat járt be azóta. Számos egyszerű, néhány atomos molekulára (víz, széndioxid, ózon – hogy csak a legdivatosabbakat említsük) ma már elméleti úton a legpontosabb kísérletekkel vetekedő, esetenként azoknál pontosabb kijelentéseket lehet tenni.1 Mégis sok gyakorlati vegyész kutató mind a mai napig bizonyos szkepticizmussal tekint az elméleti kémiára. Ez a kritika azért jogos, mert a standard elméleti módszerek még manapság is csak kis molekulákra használhatók, így távol maradnak az anyagtudomány és a molekuláris biológia frontvonalában zajló kutatásoktól. Hogy lehet az, hogy ma, amikor a számítógépek rohamos fejlődésének vagyunk tanúi, számítástechnikai okokból egyáltalán gondot okozhat egy nagyobb molekula szerkezetének megértése? A probléma gyökere a standard elméleti módszerek munkaigényének „skálázódásában” rejlik. Ezen azt értjük, hogy a számításigény hogyan, milyen hatvánnyal függ a vizsgált rendszer méretétől. Sajnos az a helyzet, hogy egy többé-kevésbé megbízható kvantumkémiai módszer munkaigénye a molekula méretének 6. hatványával arányos, de a legegyszerűbb módszerek is a 3. hatványtól függenek.2 A kvantumkémia két irányban indult el, hogy ezen a súlyos skálázódási problémán segíteni próbáljon. Az első ötlet az volt, hogy mondjunk le a pontos számításokról, és vezessünk be olyan közelítéseket, amelyek révén a számítási idő megfelelően lecsökken. Ez az ötlet néha bevált ugyan, de az általános problémát két okból nem oldotta meg: egyrészt a közelítések hamar pontatlanná váltak, másrészt a legdrasztikusabb közelítésekkel sem lehetett a hatványfüggést 2-3 alá szorítani. Ezért került előtérbe napjainkban egy teljesen új számítási filozófia, amely az elméleti apparátus átalakításával ambiciózus módon egyenesen arra törekszik, hogy a számítások munkaigénye a rendszer méretének csupán első hatványától függjön, azaz a számításigény arányos legyen a mérettel.3 Mindezt úgy kell elérni, hogy a számítás pontossága ne csökkenjen. Az ilyen típusú eljárásokat nevezik „lineárisan skálázódó” módszereknek. A lineárisan skálázódó módszerek elvi alapjainak megértéséhez matematikai ismeretekre van szükség. Megpróbálhatjuk azonban egy egyszerű hasonlattal szemléltetni, hogy milyen fajta ötletek segítenek ilyen módszerek kidolgozásához. Tegyük fel, hogy egy mozivállalat a mozitermeiben lévő székeket meg akarja számoltatni, és az a kérdés, hogy mennyi számlálási munkát kell ehhez elvégezni az egyforma arányú, de más-más méretű, téglalap alakú mozitermek nagyságának függvényében. Mivel a termek hossza és szélte arányos, egy kétszer, háromszor hosszabb teremben négyszer, kilencszer annyi szék lesz. Ha most naiv módszerrel egyenként számláljuk a székeket, azt találjuk, hogy a megszámolásukhoz szükséges idő a székek számával, azaz a terem hosszának négyzetével arányos. Ez nagyon előnytelen dolog, mert egy ötször akkora moziteremben 5×5=25-ször több időre van szükségünk, hogy az összes széket megszámoljuk. A végeredményhez természetesen nincs erre szükség. Elég ugyanis megszámolni a széksorok és az székoszlopok számát (ehhez csak a terem hosszával arányos időre van szükségünk), majd ezt a két számot egyszerűen összeszorozzuk, s máris megvan a pontos eredmény. Egyetlen plusz szorzás árán „lineárisan skálázódó” módszert kaptunk a székek pontos megszámolására. Mint minden hasonlat, ez is sántít egy kicsit, hiszen a fenti ötlet alighanem egy iskolás gyereknek is hamar eszébe jut, míg az elméleti kémia lineárisan skálázódó módszerei igencsak kifinomultak. Mégis, jól látszik, hogy az ilyen eljárások kidolgozásához valamiféle szemléletváltásra, s néhány jó ötletre van szükség. Azt is mutatja a hasonlat, hogy a lineáris skálázódás elérése érdekében valami pluszmunkát kell befektetni: példánkban a sorok és oszlopok számának összeszorzását. Egy hatéves kisgyerek például, aki már ismeri a számokat, de még nem tud szorozni, kénytelen lenne a lassúbb, négyzetesen skálázódó, egyszerű leszámlálással működő eljárást választani, ha kíváncsi volna a székek számára. Ez a kvantumkémiában is így van: a lineárisan skálázódó módszerek sokszor bonyolultabbak a hagyományosnál, és végrehajtásuk során bizonyos többletmunkát követelnek. Ezért azután kis molekulákra nem is előnyös használni őket, csak olyan nagyokra, ahol a többletmunka már kifizetődik. A következőkben bemutatunk egy, a laboratóriumunkban nemrégen kifejlesztett lineárisan skálázódó eljárást (Kőhalmi et al., 2005) molekulák elektronszerkezetének meghatározására. Ismeretes, hogy a kvantumelmélet szerint egy molekula lehetséges energianívóit a molekula energiamátrixának sajátértékei határozzák meg. Ha ezeket a sajátértékeket a hagyományos matematikai eljárásokkal kívánjuk kiszámítani, az elvégzendő számítási munka a mátrix méretének köbével arányos. Ha a sajátértékek megvannak, a molekula energiája – a legegyszerűbb (ún. Hückel-) modellben – az elektronok által elfoglalt nívókhoz tartozó sajátértékek összegeként adódik. A számítástechnika mai fejlettsége mellett egy jó minőségű átlagos személyi számítógépen egy kb. 5000 atomos molekula elektronszerkezetét lehet ily módon néhány óra alatt felderíteni. Az E energiát ugyanakkor nemcsak a sajátértékek összegeként kaphatjuk meg, de az energiamátrix (H) és az ún. sűrűségmátrix (P) elemeinek összeszorzásával is: E = Sp H P, ahol Sp a mátrix spúrképzést (a diagonális elemek összegzését) jelenti. Ha M-atomos rendszert vizsgálunk, ezek a mátrixok M x M számot tartalmaznak, tehát az energia kiszámítása négyzetesen skálázódó feladatnak tűnik. A valóságban azonban a H, és sokszor a P mátrix igencsak ritka: csak kevés eleme különbözik 0-tól. Ezért a fenti mátrixszorzás műveletigénye csak lineárisan nő a molekula méretével – ehhez mindössze annyit kell tenni, hogy nem a standard mátrixszorzó eljárásokat, hanem az ún. „ritka mátrix technológiát” (Pissanetzky, 1984) alkalmazzuk. Kérdés azonban, hogy honnan kapjuk a P sűrűségmátrixot? A hagyományos eljárás után a H energiamátrix sajátérték-problémájának megoldása után, egy köbösen skálázódó algoritmussal kaphatjuk meg a (szimmetrikus) P mátrixot, amelynek matematikai tulajdonságai a legegyszerűbb esetben egy N elektronból álló rendszerre így adhatók meg: P2 = P (idempotencia), és Sp P = N, azaz a sűrűségmátrix diagonális elemeinek összege megadja az N elektronszámot. A P mátrix azonban nemcsak a sajátérték problémán keresztül határozható meg. Ismert, hogy fennáll a következő egyenlőség is: H P = P H, tehát az egzakt P mátrix felcserélhető az energiamátrixszal. Régóta kerestek olyan eljárást, amely közvetlenül a fenti egyenletek segítségével, a drága sajátérték probléma megoldása nélkül szolgáltatná a P mátrixot. A fenti egyenletek közvetlen megoldása reménytelen ugyan, de a jó P mátrix megkapható az alábbi iterációs eljárással: Pi+1 = Pi + c PiH (1 – Pi), amelyről kimutatható, hogy az iteráció során megőrzi a P mátrix idempotenciáját is, és a diagonális elemeinek összegét is. Ebben a képletben c tetszőleges szám, amelynek alkalmas megválasztásával az iteráció gyorsítható. A P mátrix szimmetrikusságának a fenti képlet által előre vetített sérülése egy további trükkel kiküszöbölhető. Látjuk, hogy a formula alkalmazásához csupán egyszerű mátrixszorzásra van szükség, ami ritkamátrixos technológiát alkalmazva lineárisan skálázódó művelet. A fenti képletek, mint írtuk, a legegyszerűbb (Hückel-) esetre vonatkoznak. Segítségükkel több tízezer atom problémája is rutinszerűen tárgyalható. Az igényesebb, ab initio egyelektron-modellek esetében az egyenletek kissé módosulnak, de lényegük változatlan marad. A mellékelt ábrán bemutatjuk egy max. 350 vízmolekulából álló, hidrogénkötésekkel összetartott láncra végzett ab initio számítás időigényének függését a molekulák számától. Pontosabban, csak a P mátrix megkeresésére fordított időt tüntettük fel a hagyományos, köbösen skálázódó, valamint a fent ismertetett iteratív eljárás esetében. Az utóbbi linearitása szembeötlő. (A számítások egy 64 bites személyi számítógépen történtek). Az itt bemutatott példa csupán egy a manapság górcső alá vont lehetőségek közül (lásd például Kenoufi és Polónyi, 2004). Azt, hogy melyik eljárás lesz a legjobb, és végül is mikor érjük el a felvezetésben vázolt célt, hogy makromolekulákra is tudunk prediktív erejű kijelentéseket tenni, még nem látjuk pontosan, de annyi bizonyos, hogy évtizedekben mérhető kutatási ráfordításra van még szükség. Mégis, hallatlanul izgalmas kalandról van szó, ami talán végleg összekapcsol majd olyan tudományterületeket, mint a fizika, a kémia és a biológia.
Kulcsszavak: makromolekulák, kvantumkémia, skálázás, anyagtudomány, fizika, biológia, kémia

1. ábra
1 Az egyik első, kísérleti eredményeket revideáló elméleti eredményt a Nobel-díjas Gerhard Herzberg idézi, aki a saját mérési eredményeit volt kénytelen helyesbíteni később napvilágot látott számítások (Kolos – Wolniewicz, 1968) miatt. Ezt az elméleti sikersztorit Herzberg annyira lényegesnek minősítette, hogy erről tartotta székfoglaló előadását a Pápai Tudományos Akadémián is (Herzberg, 1971).
2 Egy számpéldát idézünk annak megvilágítására, hogy mekkora bajt is jelent ez. Tegyük fel, hogy elvégeztünk egy számítást egy molekulára, amelyhez mondjuk tíz órán át kellett pörgetnünk a számítógépet. Ha most egy kétszer akkora molekulát szeretnénk megérteni, akkor ehhez 26 x10 = 640 óra, tehát csaknem egy hónap számítási idő kellene. Egy ötször akkora molekulához pedig több mint tizenöt év! Megfordítva, ha tudnánk is egy tízszer gyorsabb számítógépet vásárolni, azon mindössze 610=1,47-szer nagyobb molekulára tudnánk ugyanannyi idő alatt ugyanolyan számítást végezni.
3 Részletesen: egy kétszer akkora molekulához csak kétszer annyi időre legyen szükség – ennyi munka talán még tolerálható…
IRODALOM Herzberg, Gerhard (1972): Experimental Tests of the Quantum Theory of Molecular Hydrogen. Commentarii Pontifica Academia Scientiarum. II, 49, 1. Kenoufi, Abdelouaheb – Polónyi János (2004): Projection Method for Rapid Ab Initio Calculations of Metals. Physical Review B. 70, 205105. Kolos, Wlodzimierz – Wolniewicz, Lutoslaw (1968): Improved Theoretical Ground-State Energy of the Hydrogen Molecule. Journal of Chemical Physics. 49, 404–410. Kőhalmi Dóra – Szabados Ágnes – Surján Péter (2005): Idempotency-conserving Iteration Cheme for the One-Electron Density Matrix. Physical Review Letters. 95, 13002.
Pissanetzky, Sergio (1984): Sparse Matrix Technology. Academic Press, London
<-- Vissza a 2006/5 szám tartalomjegyzékére
<-- Vissza a Magyar Tudomány honlapra
[Információk] [Tartalom] [Akaprint Kft.]