Súlyozott hálózatok:
A tőzsdétől a mobiltelefóniáig
Kertész János
az MTA levelező tagja
Budapesti Műszaki és Gazdaságtudományi Egyetem Fizikai Intézete
kertesz @ phy.bme.hu
Bevezetés
A komplex rendszerek sok kölcsönható egységből állnak, de a teljes rendszer viselkedése nem érthető meg csupán a kölcsönhatások egyre alaposabb feltérképezéséből: az egész több részeinek összegénél. A hálózati megközelítés ezért abból a leegyszerűsítő feltételezésből indul ki, hogy érdemes az egész rendszer vázával – a hálózattal – megismerkedni, a szerkezet és a funkcionalitás összefüggéseit elemezni ahelyett, hogy egyre mélyítenénk a kölcsönhatásokra vonatkozó ismereteket. Ez az elképzelés alapvető felismeréseket eredményezett az elmúlt években – ugyanakkor az is világos, hogy a valódi megértéshez a holisztikus megközelítést ötvözni kell a kölcsönhatásokra összpontosító redukcionizmussal.
Egy súlyozatlan hálózat (gráf) csúcsokból és élekből áll, és az élek binárisak: ha van kölcsönhatás két elem (illetve az őket jelképező csúcsok) között, akkor az él létezik, különben nem. A kölcsönhatások azonban egészen különböző erősségűek lehetnek, és hatásuk a működésre nagyon eltérő lehet. Látni fogjuk, hogy éppen a rendszerek komplexitása következtében nem lehet abból kiindulni, hogy a gyenge kölcsönhatások elhanyagolhatóak. Ha a valamilyen skálán jellemzett kölcsönhatások erősségét súlyként rendeljük a kölcsönhatásokat jelképező élekhez – súlyozott hálózatot hozunk létre.
Azon hálózatokban, amelyeken forgalom játszódik le (közlekedés, internet, telefonhálózat), természetes súlyként adódik az időegységre vetített forgalom. A hálózatokat gyakran valamilyen komplex rendszer alkotóelemein lejátszódó folyamatok kovarianciájának segítségével nyerjük – ilyenkor nyilván a kovariancia mértéke azonosítható az élhez tartozó súllyal. Szociális hálózatokban sokszor a kapcsolatok intenzitását tekintik a súlyok alapjának. Korreláció lehet negatív, egy kapcsolat jellemezhető ellenszenvként – látszik tehát, hogy esetenként a súlyok lehetnek negatívak is.
A súlyozott hálózatok jellemzéséhez célszerű általánosítani a súlyozatlan hálózatokra bevezetett mennyiségeket. Ilyenek a csomósodási együttható (clustering coefficient), vagy a motívumok statisztikája. A csomósodási együttható egy csúcson azt méri, hogy figyelembe véve a szomszédok adott számát, az elvileg lehetséges háromszögek hányad része valósul meg a hálózatban. Ez a szám, amely 0 és 1 között változhat, azt mutatja, hogy mennyire hajlamosak a „barátok egymással barátkozni”. A motívumstatisztika egy (véletlen) referenciamodellhez viszonyítva jelzi, hogy egy adott topológiájú részgráf szignifikánsan gyakori-e a vizsgált hálózatban. Ha igen, akkor feltehető, hogy a részgráfnak fontos szerepe van a működésben.
Ezek a fogalmak viszonylag egyszerűen általánosíthatók súlyozott hálózatokra, különösen pozitív súlyok esetén. Bevezethető a részgráfok intenzitása (a súlyok mértani közepe) és koherenciája (súlyok mértani és számtani közepeinek hányadosa), és ezek segítségével definiálható a súlyozott motívumstatisztika és a súlyozott csomósodási együttható. Ezek a fogalmak érdekes betekintést adnak a súlyozott hálózatok szerkezetébe: például kiderült, hogy a súlyok figyelembe vételével a motívumstatisztika gyökeresen megváltozhat, és a korábban a működés szempontjából relevánsnak tartott részgráfok elveszíthetik a jelentőségüket, míg mások fontossága ugrásszerűen megnőhet (Onnela et al., 2005).
A továbbiakban a technikai részletek messzemenő mellőzésével két területen elért eredményeket foglalunk össze.
Tőzsdei korrelációk hálózata
A tőzsdéken ma már minden tranzakciót feljegyeznek, és a likvid részvényekre néhány másodpercenként van kötés. Ennek megfelelően hihetetlen mennyiségű adat gyűlik össze, és joggal lehet remélni, hogy ezek tanulmányozása segíti a pénzügyi folyamatok megértését. Ugyanakkor nemcsak a kíváncsiság kielégítéséről van itt szó, hiszen olyan kérdések megválaszolásánál, hogy milyen az optimális portfólió, amely adott várható hozam mellett minimalizálja a kockázatot, az ún. történeti (vagyis a feljegyzett) adatokra kell támaszkodni.
Éppen a portfólió optimalizálása miatt kulcsfontosságú, hogy összehasonlítsuk a különböző részvények árfolyamainak mozgását. Nem érdemes olyan részvényeket a portfólióba választani, amelyek árfolyamai nagyon együtt mozognak, mert ezek nem csökkentik a kockázatot: ha az egyik ára zuhan, a másiké is fog. Az „együtt mozgás” mértékét a kovariancia együttható méri. Ha N részvényünk van, akkor a kovariancia együtthatókból előáll az N×N-es kovariancia mátrix. Általános tapasztalat, hogy mivel a mérések véges idejűek és a folyamatokban időnként trendek érvényesülnek, a kovariancia mátrix elemei nem egyforma súlyú információt hordoznak, jelentős a zavaró zaj.
Az információtartalom mértékét sok módszerrel vizsgálták, és kiderült, hogy a hálózatelméleti megközelítés érdekes eredményekre vezet. A kovariancia mátrix egy teljes súlyozott gráfként ábrázolható: a csúcsokat a részvények alkotják, minden élt két különböző csúcs között behúzunk, és a rajtuk megjelenő súlyok éppen a kovariancia mátrix megfelelő elemei. Az első célunk az, hogy meghatározzuk az egymáshoz hasonló elemek csoportjait. Ez általános probléma, amely a biokémiai kísérletsorozatok kiértékelésétől a számítógépes képfelismerésig számos helyen jelentkezik: hogyan lehet egy N elemű halmazban hasonlósági csoportokat definiálni, ha páronként ismerjük az elemek közötti hasonlóságot.
A tőzsdei adatok esetében igen hatékonynak bizonyult lehetőség, hogy meghatározzuk az ún. minimális feszítőfát (Mantegna, 1999; Onnela et al., 2003). Mindenekelőtt transzformáljuk a súlyokat a hasonlóságról (kovariancia) egy távolság jellegű mennyiségre, ami akkor a legkisebb (0), amikor a hasonlóság a legnagyobb, és így határozzuk meg a minimális feszítőfát. Ez egy részgráfja az előbbi teljes gráfnak, ami fa (nem tartalmaz hurkokat), feszítő (minden csúcs része) és minimális (az összes feszítőfa közül az, amelyiken a távolságok összege a legkisebb). Hatékony algoritmusok ismertek a minimális feszítőfa meghatározásához.
Az eredmény a tőzsdei adatok esetében nagyon érdekes (1. ábra). Kiderül, hogy a fa szerkezete jól tükrözi a gazdaság taxonómiáját: az azonos ágazathoz tartozó részvények a fa azonos ágaira kerülnek. A centrumban egy óriásvállalat, a vizsgált New York-i tőzsdén például az idő jelentős részében a General Electric van. Megmutatható, hogy az optimális portfólióba célszerű a „részvényfa” külső leveleit nagyobb súllyal választani. Ha az így megszerkesztett fa időfejlődését nézzük, akkor azt a megfigyelést tehetjük, hogy egy olyan periódusban, amikor a tőzsde csőd miatt erősen korrelált, a fa szerkezete drámai módon, mintegy fázisátalakulásszerűen megváltozik (1. ábra).
Egy másik egyszerű és hatékony eljárás a súlyozott hálózatok elemzésére a „küszöbölés” (Onnela et al., 2004). Ilyenkor a hálózatban figyelmen kívül hagyjuk az egy bizonyos küszöbérték alatti (vagy feletti) súly-lyal rendelkező éleket. Az így keletkező részgráf érdekes tulajdonságú lehet, és sokat elárulhat az eredeti hálózatról. A küszöbérték mozgatásával egy képsorozat vagy mozgókép keletkezik, amelyik az elszigetelt csúcsoktól elindulva az élek fokozatos, erősség szerinti bekapcsolásával végül a teljes hálózatig jut el. Ez a technika szoros kapcsolatban áll a perkolációelmélettel, amely a laza, elszigetelt részhálózatok és az összefüggő óriáshálózat közötti átmenetet vizsgálja. Ezzel a módszerrel elemezve a New York-i tőzsde legnagyobb vállalatai árfolyamváltozásainak kovariancia mátrixa alapján létrehozott hálózatot, kiderül, hogy bizonyos gazdasági ágazatokon belül (például ilyen az energiaszektor) nagyon erős a korreláció, míg más szektorok (például a pénzügy) elemeire ágazatokon átívelő szoros kapcsolatok jellemzőek (2. ábra). Az ilyen információk egyrészt hozzájárulnak a piac alaposabb megértéséhez, de felhasználhatók a portfóliók optimalizálásánál is.
Szociális hálózat konstrukciója és elemzése mobiltelefon-beszélgetések alapján
A modern kommunikációs médiumok minden adatot rögzítenek. Ha e-mailt küldünk, ha telefonálunk, vagy sms-ezünk, nyilvántartásba kerülnek a kapcsolatfelvétel paraméterei. Ez az adatkezelési és személyiségi jogi szempontból talán hátborzongató tény óriási lehetőségeket rejt magában a tudományos kutatás számára, amelynek során természetesen a jogi és etikai követelményeknek mindenkor messzemenően meg kell felelni.
Egy sok millió felhasználót kiszolgáló mobiltelefon-szolgáltató által rendelkezésünkre bocsátott hatalmas adathalmazt vizsgáltunk (Onnela et al., 2006). Az adatok kéthetes szakaszokra bontva tartalmazták egyéb adatok mellett, hogy ki hívott kit, és mennyi ideig beszéltek egymással. Természetesen az előfizetőket nem név vagy telefonszám, hanem kódok alapján azonosítjuk. A hálózatot kézenfekvő úgy megalkotni, hogy az előfizetők képezik a csomópontokat, és az egymással folytatott beszélgetések az élek, amelyeken a súly a beszélgetések hossza, amit a kapcsolatok intenzitása mértékének tekintünk. Az így létrejövő hálózat nem képezi le tökéletesen a társadalmat, mégis a társadalmi hálózat egy közelítésének tekinthetjük. Erre feljogosít a mobiltelefonok hihetetlen elterjedtsége (a vizsgált európai országban 2003-ban a lakosság 90 %-ának volt mobiltelefonja). Óriási előnye ennek a megközelítésnek, hogy az eddig vizsgált legnagyobb szociális hálózatot vizsgálhatjuk, amelyben ráadásul a súlyok nem megkérdezés alapján valamilyen skálán szubjektív megjelölés útján jöttek létre, hanem mért adatokból származnak (3. ábra).
Egyik feladatunknak tekintettük, hogy ellenőrizzük a szociális hálózatokban szereplő kötésekre vonatkozó, Mark Granovettertől származó és széles körben ismert, de megfelelő adatok hiányában csak hipotézisnek tekinthető állítást (Granovetter, 1973). Az erős kötések (intenzív kapcsolatok) esetében nagy átfedés van az ismerősök között, míg az átfedés kicsi, ha a kapcsolat laza. Mindenekelőtt definiálni kell az átfedést, ami értelemszerűen a közös ismerősök és a lehetséges közös ismerősök hányadosa.
A 4. ábra mutatja az egész hálózat vizsgálata alapján nyert eredményt. Eltekintve a kötések legerősebb 5 %-ától, a Granovetter-hipotézist sikerült igazolni. Ez a társadalom szerkezetéről a következő képet sugallja: A közösségek erős, sokirányú kapcsolatokkal kötődnek egymáshoz, és ezeket a közösségeket gyengébb kapcsolatok fűzik össze (lásd a 3. ábrát). Mi a helyzet a kimaradó 5 %-kal? Nos, „fakó minden teória, s a lét aranyló fája zöld” – vagyis a helyzet természetesen bonyolultabb a fenti, egyszerű képnél. Megmutattuk, hogy ahogyan közeledünk az egyre nagyobb súlyokhoz, vagyis az egyre hosszabb telefonálási időkhöz, éppen a felső 5 %-ban a partnerek elkezdenek szinte kizárólag egymással beszélni, és (hogy a fizikából származó hasonlattal éljünk) kötött párokat képeznek. Mindenkinek saját élettapasztalatából támadhatnak ötletei az ilyen kötött párok természetéről. Ezekre nyilván nem érvényes a Granovetter-hipotézis.
Mit tanulhatunk az itt feltáruló képből? Az emberi kapcsolatok kialakításának for-mái az ősidőkre nyúlnak vissza, és ez a társadalom szerkezetét nagyban meghatározza, még akkor is, ha a technika fejlődése hihetetlen új lehetőségeket teremtett. Hiába lehet ma egyetlen este, ki sem mozdulva a lakásunkból új „chat”-partnerek tucatjaival érintkezésbe lépni, az emberek túlnyomó többségének csak néhány igazán szoros kapcsolata van. A jó ismerősök száma is erősen korlátozott: a magántelefonkönyvek bejegyzéseinek nagyságrendje száz, amiből csak egy töredék a rendszeresen hívott szám. A társadalom hálózatos szerkezete ezeket a szociális képességeket és lehetőségeket tükrözi, amelyek egy hosszú fejlődéses optimalizáció révén jöttek létre. Az optimalizáció a kis közösségek hatékonysága és a stabilitás irányába mutat, és például egyáltalán nem működik az információterjedés vonatkozásában. Modellszámítások segítségével bebizonyítottuk, hogy az információ vagy akár pletyka (Szvetelszky, 2002) a közösségekben csapdába esik, és csak sokára szivárog tovább, de akkor hirtelen újabb közösséget ér el. A feltérképezett hálózat alapján stratégiákat lehet kidolgozni a terjedés hatékonyságának növelésére, amit a reklámszakmától a politikáig széles körben alkalmazni lehet – más kérdés, hogy ezt kívánatosnak tartjuk-e.
Összefoglalás
A modern médiumok óriási adatmennyiséget gyűjtenek össze az élet számos területéről. Ezen adathalmazok a tudomány számára valóságos kincsesbányát jelentenek. Egyes esetekben (telefonadatok) a jogi és etikai problémákra különös gondot kell fordítani, más esetekben (tőzsdei adatok) a feljegyzések nyilvánosak vagy megvásárolhatók. A hálózati megközelítés igen hatékonynak bizonyult az adatok forrásaként azonosítható komplex rendszerek vizsgálatában.
Az itt ismertetett kutatások nemzetközi együttműködésben folynak, amelyben részt vett: Jukka-Pekka Onnela, Jari Saramäki, Jörkki Hyvönen, Anirban Chakraborti és Kimmo Kaski (Helsinki University of Technology), Barabási Albert-László, David Lazer és Szabó Gábor (Harvard); köszönettel tartozom nekik. A munkát részben az OTKA (T49238, K60456) finanszírozta.
Kulcsszavak: komplex rendszerek, korrelációk, részvénypiac, súlyozott hálózatok, társadalmi hálózatok szerkezete
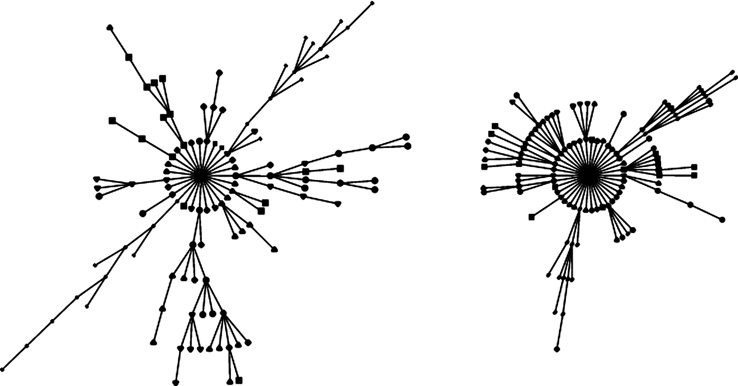
1. ábra • A tőzsdei árfolyamváltozások kovariancia mátrixából nyert minimális feszítő fák. Az egyes ágak erősebb kapcsolódást jelentenek, a piac taxonómiája jól felismerhető, amit a különböző szimbólumok érzékeltetnek. A bal oldali ábra a normális piaci helyzetet, a jobb oldali a csőd idején felerősödő korrelációk következtében „összeugró” fát mutatja.
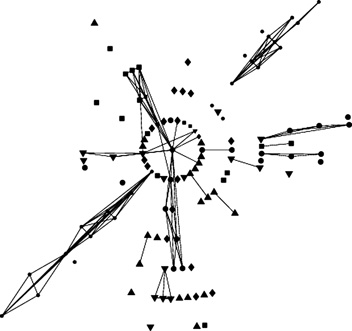
2. ábra • A küszöbölés eredménye az 1. ábra jobb oldalán bemutatott minimális feszítőfa alapjául szolgáló kovariancia mátrix felhasználásával; az egyes csúcsok elhelyezése is az ottaninak felel meg. A küszöbérték legerősebben korrelált 120 él behelyezését engedi meg, ami hasonló az 1. ábrán látható élek számához. Egyes szektorok erősen „huzalozottak” (energia), mások ezen a szinten alig (szolgáltatások).
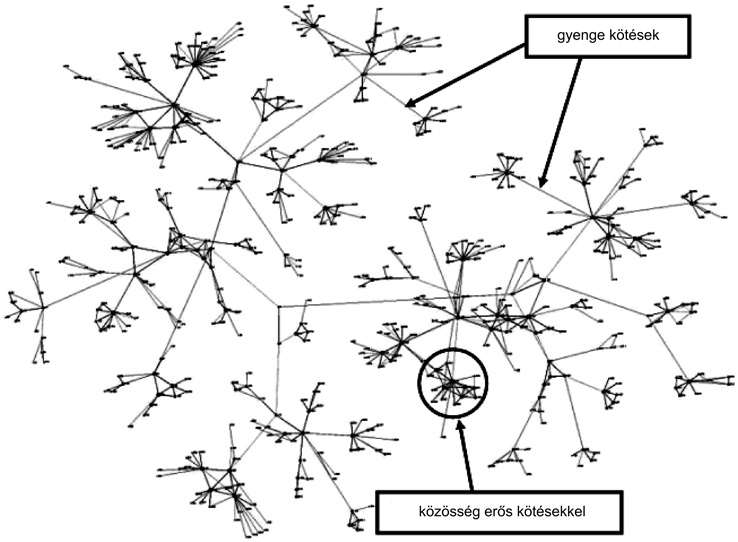
3. ábra • A mobiltelefon-hívások alapján készített hálózat kis részlete. A közösségek általában erősen „huzalozottak” – közöttük a kapcsolatot a gyenge kötések biztosítják.
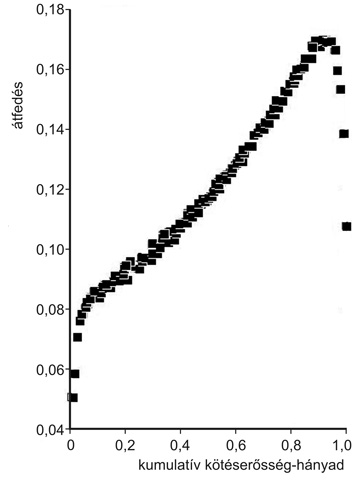
4. ábra. A Granovetter-hipotézis igazolása. A vízszintes tengelyen az erősség szerint sorba rendezett kötések hányada szerepel. A kötések 95 %-ára igaz, hogy monoton kapcsolat van a kötés erőssége és az átfedés között.
IRODALOM
Csermely Péter (2006): Weak Links. Springer
Granovetter, Mark (1973): The Strength of Weak Ties. American Journal of Sociology. 78, 1360–1380.
Mantegna, Rosario Nunzio (1999), Hierarchical Structure in Financial Markets. European Physical Journal B. 193–197.
Onnela, Jukka-Pekka – Chakraborti, A. – Kaski, K. – Kertész J. (2003): Dynamics of Market Correlations: Taxonomy and Portfolio Analysis. Physical Review E. 68, 041102.
Onnela, Jukka-Pekka – Kaski, K. – Kertész J. (2004): Clustering and Information in Correlation Based Financial Networks. European Physical Journal B. 38, 353–362.
Onnela, Jukka-Pekka – Saramaki, J. – Kertész J. – Kaski, K. (2005): Intenisity and Coherence of Motifs in Weighted Networks. Physical Review E. 71, 065103(R).
Onnela, Jukka-Pekka – Saramaki, J. – Hyvönen, J. – Szabó G. – Lazer, D. – Kaski, K, – Kertész János – Barabási A.-L. (2006): Structure and Tie Strength in Societal Networks (preprint, submitted for publication)
Szvetelszky Zsuzsanna (2003): A pletyka. Gondolat, Budapest
<-- Vissza a 2006/11 szám tartalomjegyzékére
<-- Vissza a Magyar Tudomány honlapra
[Információk] [Tartalom] [Akaprint Kft.]