Bevezetés

Napjainkban a gépjármű modellezésére mint egy összetett rendszer leírására, számos modellt és modellegyüttest használnak a mérnökök. A modellek szerepe igen sokrétű lehet, némelyeket egyszerűségük, könnyen kezelhetőségük miatt előszeretettel alkalmazzák valós időben futó szabályozások algoritmusaiban belső modellként, míg mások kimondottan szimulációkra, előzetes tesztelésekre vagy egy-egy alkatrész modellezésére lettek kifejlesztve. A környezetünk leírására megalkotott modellek két nagy csoportba sorolhatók: folytonos vagy diszkrét – elektronikai példával élve analóg vagy digitális. Általánosságban e szemlélet alapján megkülönböztethető időbeli és/vagy távolságkoordináta szerinti folytonosság vagy nem folytonosság. A folytonos modellek az anyagot folytonos közegként (kontinuumként) kezelik, azt a végtelenségig nagyítva is anyagi jellemzőkkel ruházzák fel. Ezzel szemben a diszkrét megoldás, melyet bizonyos szemszögből végeselem-módszernek is nevezhetünk, az anyagot kicsi részekre bontja, melyek tovább már nem bonthatók. A valóságban a folytonos modellek a számíthatóság miatt általában csak erőteljes megkötéssel alkalmazhatók: például tömegpontként tekinthető testek mozgása vagy egyenes csővezetékben történő homogén közeg áramlása (ilyen lehet például a hűtési folyamat előtt lévő hűtővíz áramlása). Ha azonban a mozgást végző test deformálódásra képes, vagy az áramló anyag összetétele térben-időben változó, esetleg a csővezeték alakja nem írható le folytonos függvényekkel (szabályozószelep), célravezetőbb a végeselem-módszer alkalmazása. Hasonlóképpen az aerodinamikában, például autók karosszériájának szélcsatornás tesztelésénél a közeg felfogható kontinuumként vagy ütköző levegőrészecskékként („gömbökként”), és így a newtoni fizikából ismeretes lendületmegmaradással is megalkotható egy modell, amely az eredő légellenállásra próbál becslést adni. Azonban a diszkretizálásnál legtöbbször nem érdemes az atomi méretekig lemenni, hiszen ilyen nagyszámú elem külön kezelése hihetetlen mértékben megnövelné a számítási igényeket, sőt a mai eszközökkel kezelhetetlenné válna e modellek számítása. Így a mozgó test anyagának összetételétől, alakjától vagy az áramlás milyenségétől függően a vizsgált teret különböző nagyságú térrészekre érdemes osztani, és egy-egy ilyenen belül homogén viszonyokat feltételezve vizsgálni az adott fizikai problémát.

Az időben folytonos, síkbeli és egyszerű járműmodellek csoportjába tartozik az ún. biciklimodell (Zomotor, 2006), más néven egynyomvonalú járműmodell (STM – Single Track Model), amely az adott járműre történő paraméterillesztés után a jármű függőleges tengelye körül végzett forgómozgására (perdülés, legyezés) ad becslést. A biciklimodell (Lundquist – Schön, 2009) állapotváltozói: a perdülési szögsebesség és az úszási szög, melyek szabályozási célú felhasználásával a jármű menetdinamikai tulajdonságai jelentősen javíthatók; például túlkormányzás (belső ív felé sodródás) vagy alulkormányzás (külső ív felé sodródás) esetén a jármű kanyarmenetben az ideális íven tartható. E folyamatot a magyar szakirodalom aktív perdület szabályozásnak (angol megfelelője: AYC – Active Yaw Control) hívja, mely az 1. ábrán látható módon a jármű kitörését hivatott megakadályozni.

A 2. ábrán a biciklimodell struktúrája és a modell felállításához figyelembe vett fizikai mennyiségek láthatók. A modell hat paraméterrel állítható: a tömegközéppont távolsága az első keréktengelytől (le), valamint a hátsótól (lh), a jármű tömege (m), tehetetlenségi nyomatéka (J), és a két–két összevont kerékre egy–egy kúszási merevségnek (C_e és C_h) nevezett mennyiség.

2. ábra • A biciklimodell szerkezete

és fontosabb mennyiségei

Az első két geometriai paraméter, valamint a tömeg és (eltekintve a bólintás- és dőlés- jelenségektől) a tehetetlenségi nyomaték is a járműre jellemző közel állandó értékű fizikai tulajdonságot írnak le. Ezen paraméterek értékei csupán kis mértékben változhatnak meg, például az utasszám vagy a csomagtartó terhelésének, a benzintank telítettségének függvényében (eltekintve a vontatmányoktól). Belátható, hogy a hatból utolsóként említett két paraméter, azaz a kúszási merevségek egyesítik magukban mindazon jellemzőket, amelyek az útfelület–kerék és a kerék–felfüggesztés közötti kapcsolatokat írják le. Tehát a kúszási merevségek egyesítik a felfüggesztésből, a gumi anyagminőségéből, a keréknyomás értékéből és az útburkolat minőségéből adódó összefüggéseket. A biciklimodell számtalan egyszerűsítést használ, és így megbízhatósága, pontossága korlátozott: kis kúszási szögek (~6–8°, az 1. ábrán alfával jelölve), limitált oldalgyorsulás (3–4 m/s²), és nem léphet fel hosszirányú eredő erő (közel állandó hosszirányú sebesség). Emellett a jármű mozgása során a kúszási merevségek értékei nem állandóak, ami nehezíti a modell paraméterillesztését, azaz a mérési eredményekre támaszkodva a paraméterek meghatározását optimalizálással.

A négy kerék meghagyásával a biciklimodellhez hasonló paraméterekkel rendelkező, ám egy fokkal bonyolultabb járműmodell származtatható, ahol a négy kerék mindegyikéhez tartozik egy-egy kúszási merevség. A négykerekű kétdimenziós járműmodell már jobban kezeli a hosszirányú tengelyre nem szimmetrikus hatásokat, dinamikáját tekintve azonban hasonló a biciklimodellhez. Bővítve a járműmodellt. egyre több hatás vehető figyelembe. A fő kérdés, hogy mennyire érdemes részleteibe menően egyetlen hatást figyelembe venni.

Könnyen belátható, hogy ha a jármű mozgásának szabályozása az elvárás, akkor elsőként a kerekek vizsgálata, megismerése és modellezése a sarkalatos pont, hiszen a járműre ható külső erők zöme itt, a kerék és a talaj érintkezési felülete között ébred. Két példán szemléletesen bemutatható e folyamatok fontossága. Ahogy egy jármű halad az útfelületen, a különböző kormányzási, gyorsítási és fékezési műveleteknél mind a négy kerék alakja és a rájuk ható külső erők nagysága, iránya folyamatosan változik. Mivel a tapadás során létrejövő oldalerők kanyarmenetben a kanyar középpontja felé mutatnak, és ezen erők a talaj síkjában ébrednek, így eredőjük a jármű tömegközéppontjára forgatónyomatékot fejt ki, méghozzá azt a kanyarból kifelé döntve. Ekkor a külső íven lévő kerekek terhelése jelentősen megnövekedhet, míg a belső íven lévőké jelentősen csökken, például fokozatosan élesedő kanyar esetén. Intenzív fékezésnél a járműre ható hosszirányú erők szintén a talaj síkjában ébrednek, és eredőjük olyan forgatónyomatékot fejt ki, mintha a jármű orra akarna bukni, az első tengelyen elhelyezkedő kerekek terhelése megnövekszik, és a hátsó kerekek tapadása akár teljesen meg is szűnhet. A két példa során a megcsúszást követően egy kellő rutinnal nem rendelkező, de akár egy gyakorlott vezető is elvesztheti a jármű feletti irányítást, ha a jármű nem tartalmaz olyan elektronikus vezérlő egységeket (ECU – Electronical Control Unit), amelyek ilyen esetekben be tudnak avatkozni.

A jelen cikkben ismertetett kerékmodell célja, hogy végső formájában képes legyen visszaadni a kerekek és a talaj között ébredő külső erőket bármilyen kormányzási, hajtási-fékezési művelet esetén. Miért olyan fontos ez? Ha e négy erő ismeretes – a légellenállástól eltekintve –, a jármű menetdinamikai viselkedése a biciklimodellnél pontosabban írható le, és e mennyiségekre támaszkodva megfelelő algoritmussal szabályozhatóvá válik. A végső cél egy olyan járműmodell megalkotása, melynek segítségével a járművekben alkalmazott menetdinamikai stabilitásért felelős elektronikus vezérlőegységek (ECU) hatékonysága jelentősen növelhető.

A kerékmodell szerkezete

A járműre ható külső erők a deformálódott kerekek és a talaj közös érintkezési felületein ébrednek, ha eltekintünk a haladási sebességgel egyre erőteljesebben növekvő légellenállásból származó „fékező” és a különféle karosszériakialakítástól függő, talajra leszorító vagy emelő erőktől. Ha egy kerék terhelése növekszik, a talajérintési felülete és ezáltal a tapadása is fokozódik, ha a terhelése csökken, a felület és a tapadás is csökken. Forgó kerék esetén a gumiabroncs és a talaj alkotórészeinek egymáshoz viszonyított sebességétől is függ a tapadás. Tehát a kerék alakváltozásánál fontos szerepet kap a talajérintési felület meghatározása, és hogy e felületen hogyan oszlanak meg a külső erők, azaz milyen, a felületre merőleges normál-, és a felülettel párhuzamos érintőirányú feszültségek ébrednek. Mivel ezen erők nem egyenletesen elosztva terhelik az említett felületet, és a talajt érintő pontok sebességei egymástól különbözőek, így a kerék kerületi pontjai eltérően tapadnak vagy csúsznak, attól függően, hogy milyen lesz a talajjal párhuzamos (tangenciális) feszültségek eloszlása. Így a jármű aktuális menetdinamikai viselkedésétől függően a kerék talajérintési felületén megkülönböztethetők tapadó, csúszó és átmeneti felületrészek (Lacombe, 2000). A gumianyagok érintkezési felületén fellépő súrlódási erőket – a szennyezőanyagoktól és folyadékfilmrétegektől eltekintve – a szakirodalom (Pálfi, 2010) többnyire két részre bontja: adhéziós és deformációs (hiszterézis) komponensre. Az adhéziós komponens a két felület molekulái között kialakuló kötésekből fakad, míg a deformációs komponens a felületi érdességtől, a keményebb anyagnak a puhábba való benyomódásából, és ezen érdességcsúcsok között fellépő nyírásból származik.

A fentiek alapján a kerék és az útburkolat között lejátszódó fizikai jelenségek megértéséhez és matematikai leírásához a végeselem módszert érdemes alkalmazni, mely által a teljes kerék felépíthető a modellben definiált építőkövekből. Az alapelemek meghatározásánál a kiinduló gondolat a mechanika egyik ágából, a statikából ismeretes rácsostartós szerkezetek kialakításából eredt. Ezen szerkezetek eredetileg olyan építmények általános és kritikus terhelésének meghatározását, modellezését hivatottak megvalósítani, amelyek rúdelemekből épülnek fel, például vasúti hidak, épületek belső acélváza vagy távvezetéktartó villanyoszlopok. A 3. ábrán baloldalt az Eiffel-torony látható, középen kiemelve egyetlen tartó rúdelem, illetve a helyettesítő képe. A rugó szimbolizálja a csak rugalmas alakváltozásokat. E módszerrel a mérnökök jó közelítést kapnak a különféle terhelések során kialakuló állandósult (stacioner) alakra, illetve az elemekben ébredő belső erőkre. A rendelkezésre álló rúdelemek keresztmetszetei a tervezésnél ismeretesek, így az elemekben ébredő mechanikai feszültségekre méretezhető ezen eljárással a megépítendő szerkezet.

3. ábra • Példa rácsostartóra (Eiffel-torony),

egy elem kiragadva és helyettesítő képe.

A kerékmodell alapötlete, hogy a rácsostartóknál ismeretes rúdszerkezetek anyagi tulajdonságait – melyek összefoglalóan rugalmas tagként ismeretesek – egy csillapítási taggal kibővítve a szerkezet időbeli változása is megfigyelhető, nem csupán az állandósult, alakváltozás lezajlása utáni állapot.

Erre azért van szükség, mert különböző terheléseknél nem evidens, hogy a kerék kerületének egyes pontjai mikor és hol érintik a talajt, hiszen a kerületi pontok az alakváltozások során nem állandó távolságra vannak egymástól. A rácsostartókhoz hasonlóan tehát a kerékmodell építőelemei között szerepelnek rúdelemek, kapcsolódási pontok (idealizált csuklók) és megtámasztások (kényszerek), valamint szükséges bizonyos csomópontokhoz rendelt külső erők ismerete is. Ez utóbbira példa egy kerékre jutó terhelés (a jármű tömegének bizonyos hányada) vagy a motor által leadott és a keréktengelyre átszármaztatott nyomaték (erőpárokként kezelve). A csomópontok (kapcsolódási pontok) idealizált csuklók, azaz nem képesek nyomatékot átadni, csupán erőket. A rugós vagy rugalmas tag olyan tényezőt jelent, amely egy elem alakváltozása és a benne ébredő belső erő között teremt lineáris kapcsolatot, azaz egy konstans szorzó. E rugalmassági tényezőt szokás rugómerevségnek is hívni, hiszen elsőként a rugóknál alkalmazták e fogalmat, és ilyen elven működnek a rugós erőmérők is, ahol (bizonyos határok között) a megnyúlással arányos lesz a mérendő erő. Jelképi jelölése egy rugó, ahogy ez a 3. és 4. ábrákon is látható; betűjele: „k”, egyes szakirodalmakban jelölésük „s” (springconstant).

A rugalmassági tényező fizikai jelentése és számítása a szerkezeti anyagoknál:

ahol A^(e) az (e) elem keresztmetszet, E a Young-modulus, L az (e) elem hossza. Ebből a tagból eredően egy belső erő ébred a k(e) rugalmas tényezővel rendelkező elemben (Hooke-törvény):

ahol δ^(e) az (e) elem hosszváltozását, a megnyúlás mértékét jelenti (méter), Pk(e) pedig a rugalmas tagból eredő belső erőt, melynek iránya a terhelő külső erővel ellentétes.

A csillapítási vagy csillapító tag ennél kis mértékben összetettebb, hiszen az elem alakváltozási sebessége, annak időbeli lezajlása (az elmozdulás idő szerinti deriváltja) és az elemben ébredő belső erő között teremt kapcsolatot. A jelképi jelölése egy dugattyú, ami a 4. ábrán már a rugós taggal összevonva látható; betűjele: „c” (dampingfactor). A csillapító tag megakadályozza a végtelen gyors alakváltozás kialakulását. Minél gyorsabb, minél intenzívebb az alakváltozás, azaz minél gyorsabb a terhelő külső erő változása, annál nagyobb belső erő ébred a csillapítási tagból eredően:
 

ahol δ(e) a rúdelem hosszváltozásának sebességét jelöli. A csillapítási tag kifejezése anyagi jellemzőkkel nem olyan evidens, mint a rugalmas tagnál. Ami azonban megállapítható, hogy különböző hosszúságú. de azonos anyagú elemeknél hasonló viselkedést feltételezve (arányos megnyúlás) a csillapítási tagnak is fordítottan arányosnak kell lennie az elem hosszával.

4. ábra • Párhuzamosan kapcsolt rugalmas

és csillapító tag

A 4. ábrán látható egy tetszőleges rúdelem jelképi jelölése, ilyenekből épül fel az 5. ábra kerékmodellje. A rugalmas és csillapító tagot azért érdemes párhuzamosan kapcsolni, mert így hosszuk és megnyúlásuk is azonos lesz, és így egy változóval felírható a rúdelem differenciálegyenlete, a (4) egyenlet szerint (az alakváltozásnál a megnyúlás sebessége a megnyúlás mértékének idő szerinti deriváltja).

A síkbeli kerékmodell jelenlegi formája az 5. ábra bal oldalán látható, a jobb oldali részlet pedig a tervezett térbeli modell kialakítását szemlélteti. E cikk csak a sík kerékmodellt részletezi.

A rácsostartókra igaz még – ahogy a kerékmodellre is –, hogy minden elemben csupán rúdirányú és a rudak szimmetriatengelyén áthaladó hatásvonalú¹ belső erő ébredhet. E belső erők az alakváltozásból (δ), és az alakváltozás sebességéből (δ)erednek, és e két hatás összege adja a vizsgált elemben ébredő teljes belső erőt (P(e)) (felsőindex: egy elemre vonatkoztatva). Így a (2) és (3) egyenlet összegéből következik:
 

A modellt alkotó rúdelemeknek nem szükséges ismert vastagsággal rendelkezniük, azonban az (1) egyenlet alapján minden rúd rendelkezik keresztmetszettel és Young-modulussal (húzó rugalmassági modulus). Ezek pontos ismerete a modell számára nem lényeges, ugyanis a k és c paraméterek illeszthetők. A tényezők szempontjából lényeges tulajdonságok egy adott méretű kerékre ismertek, melyek a geometriai jellemzők (a fellni és az abroncs sugara) és a modell finomságától (N szögosztástól) függő L(e) elemek hosszai.

A dinamikai viselkedés szempontjából elengedhetetlen, hogy a rendszer rendelkezzen tömeggel. Terhelésnél értelemszerűen a keréktengelyre helyezett tömeg a domináns, azonban a csomópontokba helyezett kis tömegekkel a kerék súlya is figyelembe vehető. A jármű súlyához viszonyítva e kicsi tömegek a rendszer dinamikáját gyakorlatilag nem befolyásolják, így akár el is hanyagolhatók.

Belátható, hogy egy eredetileg terheletlen, majd a 0. időpillanatban terhelő erőkkel rendelkező szerkezet esetén a kezdeti időpontban minden erő a szerkezet tömegének gyorsítására fordítódik. A folyamat kezdetekor az elemekben ébredő belső erők lényeges része az alakváltozás sebességéből ered, hiszen ekkor még az elemek nem rendelkeznek számottevő megnyúlással. Ezt követően fokozatosan az alakváltozásból eredő belső erő veszi át a meghatározó szerepet, és a folyamat egészen addig tart, amíg az alakváltozás megáll, a kerék felveszi végső alakját, amikor is a csomópontok gyorsulása és elmozdulási sebessége nulla lesz. Ez az eset természetesen akkor áll fenn, ha a kerék állandósult állapotában álló helyzetben marad, például sík talajon az álló jármű súlyának negyede terheli az egyik kereket, vagy gyorsítás után, fékezés hatására a kerék megáll. Ha az állandósult állapotban a kerék egyenletes szögsebességű forgómozgást végez, a modellt alkotó elemekben periodikus folyamatok zajlanak le.

A korábbi gondolatmenetet folytatva, a kerék szerkezete teljes egészében modellezhető ilyen rugalmas és csillapítási tagokkal felruházott elemekkel. Az 5. ábrán a különböző árnyalatú pöttyök és vonaltípusok különböző rugalmas és csillapítási tagokat jelölnek. A jelölés megválasztása csupán a szemléltetést szolgálja. Fontos megjegyezni: a fellni és a gumiabroncs eltérő szilárdsága is kezelhető ilyen elemekkel úgy, hogy két-három nagyságrenddel merevebb jellemzőkkel rendelkeznek a felnit alkotó elemek. A rugalmas és csillapítási tagok segítségével a gumiabroncs és a fellni anyagának eltérő viselkedése is leírható; például ha a két anyag rugalmas és csillapító tagjainak arányai eltérnek, más dinamikájúak lesznek: gyors és minimális deformáció, vagy lassú, de jelentős alakváltozás. Ha az abroncs kerületi (az 5. ábrán sötét pöttyök) és sugárirányú (világosabb pöttyök) elemeinek anyaga azonos, a hosszúságuk eltérősége miatt – akárcsak a különböző hosszúságú, de azonos anyagú rugóknál, az (1) egyenlet alapján – a rugalmas és csillapítási tényezőjük különbözni fog (az ábrán más árnyalattal vagy vonaltípussal jelölve). Emellett egyes abroncskerületi pontokhoz nem egy, hanem két darab abroncs sugárirányú elem (későbbiekben: belső elem) csatlakozik (5. ábra). A duplázott elemek rugalmas és csillapítási tulajdonsága nagy N szögosztásértékekre megközelítően a fele a szimpla elemek rugalmas és csillapítási tényezőinek, amivel a kerékmodell számol, de az 5. ábrán az átláthatóság érdekében ez nincs külön megjelölve.

A kerékmodellt alkotó szerkezeti elemek nem rendelkeznek önsúllyal, mert a kerületi elemek dinamikai tulajdonságának megőrzése érdekében, ahogy a rugalmas tag is fordítottan arányosan nő a hossz csökkenésével, úgy a tömeg is ezt tenné. A rúdelemek önsúlyának elhanyagolásából származó számolási hiba elhanyagolhatóan kicsi – a kerék és a jármű tömege közti nagyságrendbeli eltérés miatt –, azonban magasabb haladási sebességeken valószínű, hogy a fellni tömegének, tömegeloszlásának szerepe jelentőssé fog válni. Ebben az esetben a korábban említett módon a tömeg nélküli csomópontokhoz – őket átalakítva tömegközéppontokká – tömeg rendelhető.

Megvalósítás

A kerékmodell tárolja az elemek és csomópontok kapcsolódási viszonyait, a kerék kezdeti geometriáját (5. ábra), illetve az aktuális megtámasztásokat (kényszereket), azaz hogy mely csomópontok érintik a talajt, és e pontoknál milyen deformációk jöttek létre a talaj anyagában. Ezek alapján minden időpillanatban számolja a kerékmodell a csomópontok gyorsulásait, sebességeit és elmozdulásait, majd ezekből az elemekben ébredő belső erőket, valamint a talaj és gumiabroncsrészek között létrejövő érintő- és merőleges irányú erőket.

A számítási algoritmus maga a kerékmodell lelke, lényegében az elmozdulás módszer van átszabva és kibővítve az aktuális mechanikai problémára. A kerékmodell minden egyes csomópontra egyensúlyi egyenleteket ír fel, amelyeket „összegezve” megkapja a teljes szerkezet differenciál-egyenletrendszerét. Ehhez szükség van a rúdelemek lokális koordinátarendszeréből (minden rúdelemnél egyéni, és időben változó) való áttérésre a kerékmodell globális koordinátarendszerébe (az 5. ábra és a 6. ábra koordinátarendszere). Az elemek lokális koordinátarendszerében a megnyúlás egy dimenzióban történik, mindig a rúd hatásvonalán. E hatásvonal Θ állásszöge azonban változhat, így célszerű a rúdelemet közrefogó csomópontok elmozdulását tekinteni, és ezeket függőleges és vízszintes irányú komponensekre bontani. Így bármely rúd megnyúlása felírható a közrefogó csomópont négy elmozduláskomponensével. Az (5) egyenletben a két tetszőleges i és j csomópontok által közrefogott elem megnyúlása látható:

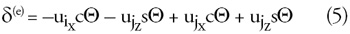
ahol cΘ a koszinusza, sΘ pedig a szinusza a Θ állásszöggel rendelkező rúdelemnek (6. ábra). Az (5) egyenletet deriválva a megnyúlás sebessége is megkapható, majd ezeket a (4) egyenletbe beírva, és a szögfüggvényeket az elem anyagi tulajdonságaival együtt két mátrixba foglalva:

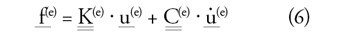
Az összes elemre felírható ezen egyenletrendszer, majd ezeket csomópontonként összegezve a csomóponti egyensúlyi egyenletrendszerek is, melyeket egységes formába rendezve a teljes rendszer egyenletrendszere is megalkotható.

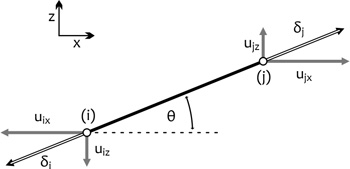
6. ábra • Az i és j tetszőleges csomópontok

által közrefogott rúdelem

Erre egy egyszerű példa (a 7. ábra bal oldali részlete), ha egy rugót felfüggesztve, majd F erővel terhelve a rugóban csupán rugóirányú erők ébredhetnek, így a rugó szimmetriatengelye egybe fog esni a terhelő erővel. Ekkor nem szükséges a lokális-globális koordinátarendszerek használata, elég, ha az erő hatásvonalának egyenese van csupán figyelembe véve, és az ébredő belső erő nagysága megegyező a terhelő erővel.

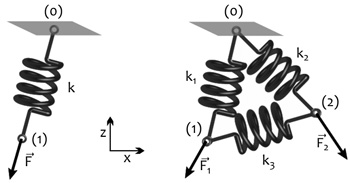
7. ábra • Egyetlen rugó és háromszögbe

kapcsolt rugók terhelése

Ha azonban három rugót a végeiknél összekapcsolunk (a 7. ábra jobb oldali részlete), e kapcsolódási pontokból egyet felfüggesztve és így terhelve a másik két kapcsolódási pontot, már nem lehetséges a problémát az előző esetben tapasztalt evidens módon megoldani, csak részekre bontással, csomóponti egyensúlyi egyenletekkel. Eszerint minden – a példában a (0), (1) és (2) – csomópontra fel kell írni a vektoriális erőegyensúlyt, ahol a belső erők tovább bonthatók a (2) egyenlet szerint. Ezután (síkbeli esetet feltételezve) minden erő felbontható függőleges, z-irányú és vízszintes, x-irányú komponensekre – a (6) egyenlet szerint, csak a csillapítós tagot elhagyva –, így minden csomópont esetén két egyensúlyi egyenlet lesz, a két komponensnek megfelelően. Az összes csomópont mindkét irányú komponensét tartalmazza az f külső erők, és az u csomóponti elmozdulások vektora a (7) egyenlet szerint.
 

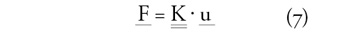
A 7. ábra jobb oldali példáját tekintve a vektorok hossza 6, a K mátrix mérete pedig 6×6, amely nem csak az elemek rugalmas tényezőjét, hanem az elemek helyzetét is magába foglalja. Tehát globálisan szemlélve a problémát, nemcsak az elemek merevségétől (rugós tag), azaz az anyagi jellemzőiktől függ, hanem a helyzetüktől, a globális koordinátarendszerben vett állásszögeiktől is.

A folyamatot nem részletezve, a kerékmodell elemeire nézve, kiegészítve a (6) egyenletet a csomópontokban elhelyezkedő tömegekkel, a csomóponti erők szerint az alábbi mátrixos formába rendezhető a teljes rendszer egyensúlyi egyenletrendszere:

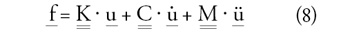
ahol f, u és deriváltjainak vektorai már a rendszer összes csomópontjának függőleges és vízszintes komponenseit magukba foglalják. Tehát a (7) és (8) egyenletekben már nincs (e) felsőindex, hiszen ezek nem egy-egy elemre, hanem a teljes szerkezetre vonatkoznak. Természetesen, ha egyedül a kerék középpontjába helyezett terhelés (mint tömeg) van figyelembe véve, akkor az M tömegmátrix csupán két elemet tartalmaz (x és z irányú komponense a kerékközépponthoz kapcsolódóan).

Egy másik példában két rugót párhuzamosan felfüggesztve, végpontjaikat egy elemmel összekötve, és így erővel terhelve a rugók azonos megnyúlást szenvednek. E két rugót függőlegesen szimmetrikusan, a kapcsolódási pontnál hegyesszöget bezárva és így felfüggesztve, valamint az előző esetnél használt erővel terhelve, az előző esethez képest a megnyúlás eltérő, nagyobb lesz, mert a két elemben így nagyobb belső erő ébred. A modell finomságát kifejező, részben szabadon állítható paraméter (csupán 4-nél nagyobb páros szám) a szögosztás, amely a fellni belső elemeinek számát jelenti. Ezt N-nel jelölve a modell

3N + 1                 (9)

csomópontot, és

7N                       (10)

darab elemet tartalmaz. Természetesen az N érték növelésével egy iteráció futási ideje fokozatosan növekszik, ami néhány szögosztásnál az 1. táblázatban olvasható.
 

1. táblázat

A kerékmodell a Matlab-forráskód (M-code) felületén került implementálásra, mely a C programozási nyelvhez hasonló programnyelvet használ. A Matlab használatának fő oka a vektor- és mátrixműveletek széles körű és gyors kezelése. A kerékmodell forráskódja számos olyan programozástechnikai megoldást tartalmaz, amellyel a futási idő még tovább csökkenthető. Ilyen például az egyes rúdelemek lokális koordinátarendszeréből a teljes modell globális koordinátarendszerébe történő váltás során használatos – az (5) egyenletben látható – szögfüggvények kiküszöbölése. Ugyanis elméletben ismertnek kell lennie minden egyes rúdelem szögének, majd ezek megfelelő szögfüggvényeinek kombinációjából egy „átkonvertáló” mátrixot kell képezni minden rúdelemre (e mátrix már összevonva látható az anyagi jellemzőkkel a (6), (7), és (8) egyenletekben). Itt a köztes lépések helyett a kerékmodell egy egyszerűbb és gyorsabb módszert alkalmaz.

Az idő szerepe kiemelten fontos a diszkrét idejű kerékmodell-számításában. A numerikus számítások elvégzéséhez szükséges megfelelő futási idő és pontosság biztosításához az algoritmus változó lépésközzel dolgozik. A talajérintési pontok minél pontosabb meghatározását a mintavételezési idő növelésével, míg a megfelelő futásidőt az állandósult állapot körüli mintavételezési idő csökkentésével biztosítja.

A modell tehát megszámlálhatóan sok elemre bontja a kereket; a kerékmodell ezen elemek alakváltozásait képes számolni, majd ezeket összegezve képes meghatározni a kerék alakját és az ébredő erőket a kerék anyagán belül, valamint a talaj és kerék érintkezési felületén.

Pontok talajérintése

A kényszerek vagy más néven megtámasztások a kerékmodell egyik leglényegesebb pontját képezik. A kezdeti időpillanat egy idealizált eset, amikor is a deformálódástól mentes kerék egyetlen pontban érinti a talajt – hiszen a kerék önsúlya zérusnak van véve –, ilyen formában látható a modell az 5. ábrán. A modell jelen állapotában a forgómozgást végző kereket még nem képes megfelelően leírni, így az álló helyzetben terhelt kerék alakváltozásának bemutatására kerül a fő hangsúly. A külső és belső erőktől mentes kerékmodellnél a jármű súlyának megközelítően a negyedét a keréktengelyre helyezve egy csak függőleges irányú erőkomponens terheli a modellt, megindul az alakváltozás. E folyamat a függőleges tengelyre ideális esetben szimmetrikus, és az első érintkezési ponttól a kerületen két irányban haladva az abroncs kerületi pontjai párosával érkeznek le a talajra. A deformálódás során a kerületi pontok lefelé és a z tengelytől távolodva haladnak. A leérkezés pillanatában a kerületi pontok „hozzáragadnak” a talajhoz, új függőleges (a talaj anyagának összenyomása) és vízszintes (csúszás-tapadás) kényszerek jelennek meg. A kerékmodell a talaj anyagát is a kerék anyagához hasonlóan paraméterezi, ezek a talaj szilárdságát reprezentálják. Az értékeket a felni anyagát megközelítő nagyságrendűre választva, a talaj deformációja µm nagyságrendbe esik. Ennél lágyabb anyagú talaj esetén a talajrészek deformációja egyre látványosabb, akár összemérhetővé is tehető az abroncsnál tapasztaltakkal (például homok vagy hó esetén). A kerékmodell tehát képes a talaj anyagában létrejövő alakváltozásokat is kezelni.

Álló kerék alakváltozása

A kerék középpontját terhelő nehézségi erő hatására a kerékmodellt alkotó elemekben belső erők ébrednek, a helyzetük, a hozzájuk tartozó anyagi jellemzők és a külső erő(k) függvényében. Forgómozgást nem végző kerék esetén az alakváltozás a függőleges tengelyre szimmetrikus alakot eredményez.
 

2. táblázat • A példában használt paraméterek²

A 8. ábrán jobb oldalon egy 180/60R14-es kerék síkbeli modell szerinti képe látható (a kerék nyugalmi sugara: 276,1 mm, a felnié pedig 165,1 mm), a kiindulási és a deformálódott alakjával. A példában használt szögosztás: N = 100. Az origó a deformálódástól mentes kerék talajérintési pontja.

A 9. ábrán legfelül a talajjal való érintkezési szakaszra közelítve látható a deformálódott alak. Térbeli kerékmodell esetén minden talajt érintő ponthoz rendelhető egy kis felületrész, amelyen a pontot terhelő erő megoszlik, amelyet a két anyag határán ébredő feszültségnek nevezünk. Síkbeli modell esetén a keréknek nincs vastagsága, ezáltal csupán kis szakaszok rendelhetők a pontokhoz, így mennyiségileg nem feszültséget ad a modell, hanem vonal mentén megoszló terhelést (N/m), ezért van a 9. ábrán idézőjelben az elnevezés, illetve továbbiakban feszültségként van említve a mennyiség. A 9. ábrán középen távolsághelyesen a felületre merőleges, és alul a felületre nézve érintő irányú „feszültségek” időbeli alakulása látható, amelyek a kerékre visszahatnak.

A negatív tartományban lévő feszültségek a koordinátatengellyel ellentétes irányba mutatnak, így a tangenciális feszültségek az origó felé irányulnak, a kerék csomópontjai a talajon az origótól távolodni „próbálnak”. A teljes talajérintési hosszra integrálva a normálirányú feszültségeket, megkapható a talajon ébredő erők eredője, melynek hatásvonala a szimmetria miatt az origón áthalad (a kerék középpontjára nem fejt ki forgatónyomatékot), nagysága pedig állandósult helyzetben a nehézségi erővel egyezik meg. A tangenciális feszültségek függvénye szintén szimmetrikus, így a talajon ébredő oldalirányú erők eredője zérus, a kerék álló helyzetben marad. A kilenc különböző időpontban felvett – a kerékmodell a köztes időpontokban is számolta a feszültségeket – görbéből látható, hogy a vizsgált 1,3 másodperces időintervallum első tizedében (154 ms) zajlik le a változás zöme; a két utolsó időpontbeli görbe csupán abban tér el, hogy a talajt érintő pontok enyhén kifelé csúsztak.

A 10. ábrán látható a kerék középpontjának elmozdulás–idő és sebesség–idő függvénye, melyekről felismerhető, hogy a megadott paraméterekkel ebben a példában egy túlcsillapított másodfokú rendszert ad a kerékmodell. A kerék középpontjába helyezett tömeg miatt a rendszernek van tehetetlensége, így a talajérintési ponton a normálfeszültségek ~51 ms-ig (pontvonal és jobbra mutató háromszög), a tangenciális feszültségek ~91 ms-ig (szaggatott vonal és lefelé mutató háromszög) fokozatosan növekednek, majd „szétterülve” csökkennek. Az utóbbi három ábrát összevetve látható, hogy a kerék 1,8 cm-t mozdult el a ~400 kg-os terhelés (4000N) hatására, és így a talajérintési szakasz nagysága 20 cm.

A deformációk lezajlásával kapott állandósult állapotra vonatkozó feszültséggörbék jó egyezést mutatnak más síkbeli kerékmodelleknél kapott görbékkel.

Fejlesztési irányok

A következő sarkalatos lépés nyilvánvalóan a kerék megforgatása lesz. Ehhez elkerülhetetlen a pontos meghatározása azoknak az időpontoknak, amikor a talajt érintő pontok elengedik a megtámasztásukat. E számítást már tartalmazza a modell, azonban a talajon való csúszás – a korábban említett adhéziós és deformációs állapotok – folyamatának pontosítása még hátra van.

A kerék megforgatása nem hajtott kerék esetén egy vízszintes erőkomponens segítségével történhet, vagy hajtott kerék esetén a motor által leadott és a keréktengelyre átszármaztatott nyomatékkal ekvivalens erőpárok segítségével. Az előbbi egyetlen erőt a keréktengelyre, míg az utóbbi esetben az erőpárokat a fellni kerületi pontjaira érdemes helyezni, hiszen ennek anyaga minimális alakváltozást szenvedhet csak.

A már forgásban lévő keréknél a modell képes lesz a talajon eredő erőket, a 9. ábrához hasonlóan a feszültségeket és eredő gördülési ellenállást számolni, illetve közelítést adni arra, hogy a kerék milyen fokú csúszási állapotban van, mellyel később a jármű mozgásállapotának szabályozásához is hozzá tud majd járulni.
 

Kulcsszavak: járműdinamika, egynyomvonalú,

ún. biciklimodell, kerék, gumiabroncs, menetdinamika, rugalmas és csillapító tag, végeselem-módszer
 

IRODALOM

Lacombe, J. (2000): Tire Model for Simulations of Vehicle Motion on High and Low Friction Road Surfaces. In: Proceedings of the 2000 Winter Simulation Conference. Hanover, NH, USA. 

Lundquist, C. – Schön, T. B. (2009): Recursive Identication of Cornering Stiffness Parameters for an Enhanced Single Track Model. Saint-Malo, France

Pálfi L. (2010): A súrlódás hiszterézis komponensének végeselemes modellezése gumi-érdes felület csúszó pár esetén (Phd-értekezés). Budapest

Powers, W. F. – Nicastri, P. R. (2000): Automotive Vehicle Control Challenges in the 21st Century. Elsevier

Ramajani, R. (2006): Vehicle Dynamics and Control. University of Minnesota, USA–Springer ISBN 0-387-26396-9, e-ISBN 0-387-28823-6.

Ray, L. R. (1997): Nonlinear Tire Force Estimation and Road Friction Identification: Simulation and Experiments. Automatica. 33,

Roylance, D. (2000): Trusses. Massachusetts Institute of Technology, Cambridge, MA Vable, Madhukar (2002): Mechanics of Materials. : Oxford University Press (Michigan Technological University), NY

Yung-Hsiand, J. H. – Gerdes, C. J. A (2006): Feel for the Road : A Method to Estimate Tire Parameters Using Steering Torque. AVEC ‘06, Stanford, California, USA 

Zomotor Á. (2006): Gépjármű menetdinamika.: Maróti, Bp
 

LÁBJEGYZETEK

1 Ezáltal rúdelemekben csak húzó-, illetve nyomóerők ébredhetnek a szerkezeten belül, azaz nincs nyíró, csavaró és hajlító igénybevétel, valamint a kerékmodell eltekint a kihajlás jelenségétől. <

2 Sűrűségek, amelyek N-től függetlenek, és amelyekből a k és c paraméterek származtathatók. Jelentése: a keréknél egy fok mekkora merevséget, csillapítást képvisel. <